Question

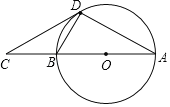
【题目】如图，CD是⊙O的切线，点C在直径AB的延长线上．

（1）求证：∠A＝∠BDC；

（2）若＝，AC＝3，求CD的长．

Answer 1

【答案】（1）详见解析；（2）2．

【解析】

（1）要证明∠A=∠BDC，只要求出∠ODC=∠BDA即可，根据题目中的条件，不难得到∠ODC=∠BDA=90°，∠ODB=∠OBD，从而可以证明结论成立；

（2）要求CD的长，只要证明△CDB∽△CAD即可，然后根据，AC=3，即可求得CD的长．

（1）连接OD．

∵CD是⊙O的切线，点C在直径AB的延长线上，

∴∠ODC=90°，∠BDA=90°，OB=OD，

∴∠ODB+∠BDC=90°，∠OBD+∠A=90°，∠ODB=∠OBD，

∴∠A=∠BDC；

（2）∵∠DCB=∠ACD，∠BDC=∠DAC，

∴△CDB∽△CAD，

∴，

∵，AC=3，

∴，

∴CD=2，

即CD的长是2．