题目内容
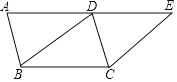
【题目】如图，将△ABC绕点A逆时针旋转得到△ADE，其中点B、C分别与点D、E对应，如果B、D、C三点恰好在同一直线上，那么下列结论错误的是（ ）
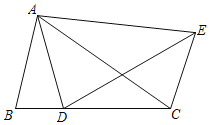
A.∠ACB＝∠AEDB.∠BAD＝∠CAE
C.∠ADE＝∠ACED.∠DAC＝∠CDE
【答案】D
【解析】
利用旋转的性质直接对A选项进行判断；利用旋转的性质得
，再利用角的和差可得
，则可对B选项进行判断；利用旋转的性质得
，然后根据等腰三角形顶角相等时底角相等得到
，则
，则可对C选项进行判断；先判断
，而
不能确定等于
，则可对D选项进行判断．
∵
绕点A逆时针旋转得到
∴
，则A选项的结论正确
由旋转的性质可得
即
∴，则B选项的结论正确
∵绕点A逆时针旋转得到
∴
和
都是等腰三角形
∵
∴
∴，则C选项的结论正确
∵
，即
又
∴
∵AD不能确定平分
∴不能确定等于
∴
不能确定等于，则D选项的结论错误
故选：D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
