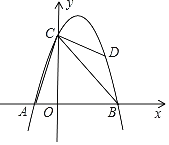
题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,![]() 为
为![]() ,点A的坐标是
,点A的坐标是![]() ,
,![]() ,把
,把![]() 绕点A按顺时针方向旋转
绕点A按顺时针方向旋转![]() 后,得到
后,得到![]() ,则
,则![]() 的外接圆圆心坐标是( )
的外接圆圆心坐标是( )
A.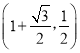 B.
B.![]() C.
C. D.
D.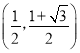
【答案】A
【解析】
取AB'中点P,过点P分别作PE⊥x轴,根据旋转的性质可得AB=AB',∠BAB'=90°,∠B'O'A=∠BOA=90°,先说明![]() 的外接圆圆心为点P,再利用点A的坐标是
的外接圆圆心为点P,再利用点A的坐标是![]() ,
,![]() ,求得AB长,进而可得AB'的长,在求得∠PAE=30°,在Rt△PAE中,利用30°角的性质及勾股定理即可求得答案.
,求得AB长,进而可得AB'的长,在求得∠PAE=30°,在Rt△PAE中,利用30°角的性质及勾股定理即可求得答案.
解:如图,取AB'中点P,过点P分别作PE⊥x轴,垂足为点E,连接PO',
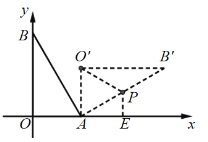
∵把![]() 绕点A按顺时针方向旋转
绕点A按顺时针方向旋转![]() 后,得到
后,得到![]() ,
,
∴AB=AB',∠BAB'=90°,∠B'O'A=∠BOA=90°,
∵点P为AB'的中点,
∴PA=PB'=PO'=![]() AB',
AB',
∴![]() 的外接圆圆心为点P,
的外接圆圆心为点P,
∵∠BAO=60°,∠AOB=90°,
∴∠ABO=90°-∠BAO=30°,
∴OA=![]() AB,
AB,
∵点A的坐标为(1,0),
∴OA=1,
∴AB'=AB=2OA=2,
∴PA=![]() AB'=1,
AB'=1,
∵∠BAB'=90°,∠BAO=60°,
∴∠PAE=180°-∠BAB'-∠BAO=30°,
∴PE=![]() PA=
PA=![]() ,
,
∴在Rt△PEA中,![]() ,
,
∴点P的坐标为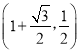 .
.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目