题目内容
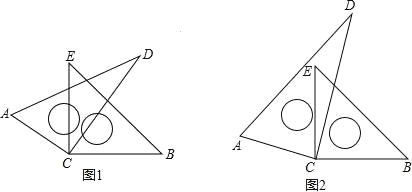
【题目】如图,直线l:y=kx+b(k<0)与函数y= ![]() (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, ![]() )、(c,
)、(c, ![]() ),其中a>c>0.
),其中a>c>0.
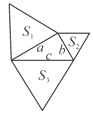
(1)如图①,求证:∠EDP=∠ACP;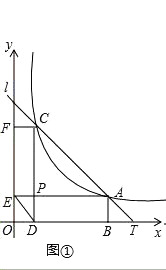
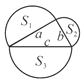
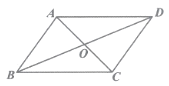
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;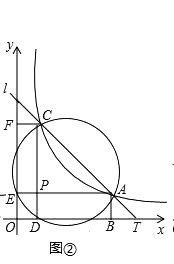
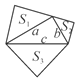
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.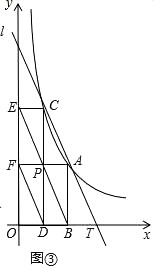
【答案】
(1)
证明:由题意可知P(c, ![]() ),E(0,
),E(0, ![]() ),D(c,0),
),D(c,0),
∴PA=a﹣c,EP=c,PC= ![]() ﹣
﹣ ![]() =
= ![]() ,DP=
,DP= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,且∠EPD=∠APC,
,且∠EPD=∠APC,
∴△EPD∽△CPA,
∴∠EDP=∠ACP
(2)
如图1,连接AD、EC,
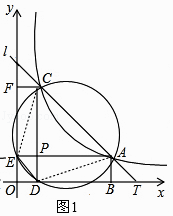
由(1)可知DE//AC,
∴∠DEC+∠ECA=180°,
∵A、D、E、C四点在同圆周上,
∴∠DEC+∠DAC=180°,
∴∠ECA=∠DAC,
在△AEC和△CDA中
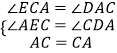
∴△AEC≌△CDA(AAS),
∴CD=AE,即a= ![]() ,可得ac=4,
,可得ac=4,
∵A、C在直线l上,
∴ 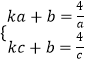 ,解得k=
,解得k= ![]() =﹣
=﹣ ![]() =﹣1
=﹣1
(3)
假设在线段AT上存在点M,使OM⊥AM,连接OM、OA,作MN⊥x轴于点N,如图2,
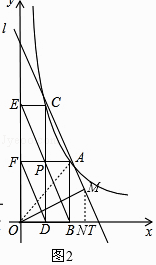
∵c=1,
∴C(1,4),F(0,4),P(1, ![]() ),B(a,0),
),B(a,0),
设直线BF的解析式为y=k′x+4,由题意可得 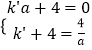 ,解得a=2,
,解得a=2,
∴A(2,2),
∴AP为△DCT的中位线,
∴T(3,0),
∴AT= ![]() =
= ![]()
∵S△OAT= ![]() OTAB=
OTAB= ![]() ATOM,
ATOM,
∴OM= ![]() =
= ![]() =
= ![]() ,
,
在Rt△OMT中,MT= ![]() =
= ![]() =
= ![]() ,
,
同理可求得MN= ![]() =
= ![]() ,
,
在Rt△OMN中,ON= ![]() =
= ![]() =
= ![]() ,
,
∵2< ![]() <3,
<3,
∴点M在线段AT上,
即在线段AT上存在点M,使得OM⊥AM,M点的坐标为( ![]() ,
, ![]() )
)
【解析】(1)由P、E、D的坐标可表示出PA、EP、PC和DP的长,可证明△EPD∽△CPA,利用相似三角形的性质可证得结论;(2)连接AD、EC,可证明△AEC≌△CDA,可得CD=AE,把A、C坐标代入直线l解析式,可求得k的值;(3)假设在线段AT上存在点M,使得OM⊥AM,连接OM、OA,可表示出C、F、P、B的坐标,利用直线BF的解析式可求得a的值,可求得A点坐标,可求得T点坐标,在△OAT中,利用等积法可求得OM的长,在RtOMT中可求得MT的长,作MN⊥x轴,同理可求得MN的长,则可求得ON的长,可判断N在线段BT上,满足条件,从而可知存在满足条件的M点.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小.

 新思维寒假作业系列答案
新思维寒假作业系列答案