Question

【题目】将一矩形纸片OABC放在平面直角坐标系中，O（0，0），A（6，0），C（0，3）．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动 秒时，动点P从点A出发以相等的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．
（1）用含t的代数式表示OP，OQ；
（2）当t=1时，如图1，

将沿△OPQ沿PQ翻折，点O恰好落在CB边上的点D处，求点D的坐标；
（3）连接AC，将△OPQ沿PQ翻折，得到△EPQ，如图2．

问：PQ与AC能否平行？PE与AC能否垂直？若能，求出相应的t值；若不能，说明理由．

Answer 1

【答案】
（1）

解：OP=6﹣t，OQ=t+

（2）

解：当t=1时，过D点作DD1⊥OA，交OA于D1，如图1，

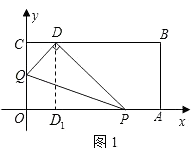
则DQ=QO= ，QC= ，

∴CD=1，

∴D（1，3）

（3）

解：①PQ能与AC平行．

若PQ//AC，如图2，

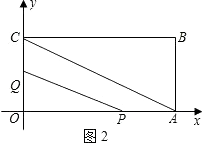
则 ，

即 ，

∴ ，而 ，

∴ ．

②PE不能与AC垂直．

若PE⊥AC，延长QE交OA于F，如图3，

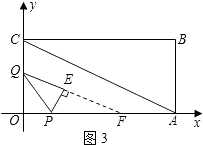
则 = ，

= ，

∴ ．

∴EF=QF﹣QE=QF﹣OQ= = =（ ﹣1）（t+ ），

又∵Rt△EPF∽Rt△OCA，

∴ ，

∴ ，

∴t≈3.45，而 ，

∴t不存在

【解析】（1）点Q运动的时间比点P多 秒，则运动的路程也多出了 ．（2）利用翻折得到的线段长，再利用勾股定理可求得点D的横坐标，纵坐标和点C的纵坐标相等．（3）当平行的时候，所截得的线段对应成比例，即可求得时间值．当垂直的时候也要找到一组平行线，得到对应线段成比例看是否在相应的范围内．
【考点精析】关于本题考查的矩形的性质和翻折变换（折叠问题），需要了解矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．