题目内容
【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 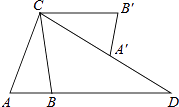
【答案】6
【解析】解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,
∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,
∵CB′∥AB,
∴∠B′CA′=∠D,
∴△CAD∽△B′A′C,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得AD=8,
∴BD=AD﹣AB=8﹣2=6.
故答案为:6.
依据图形可知∠CAB=∠CAD,然后依据平行线的性质以及旋转的性质得出∠B′CA′=∠D,故此可证明△CAD∽△B′A′C,然后依据相似三角形的性质可求得AD的长,最后,再依据BD=AD﹣AB求解即可.

练习册系列答案
相关题目