题目内容
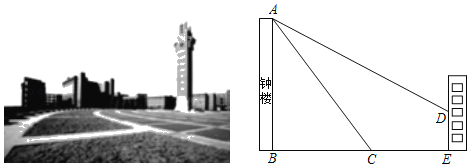
【题目】如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB=![]() ,DF=5,则BC的长为( )
,DF=5,则BC的长为( )

A.8B.10C.12D.16
【答案】C
【解析】
连接BD,如图,先利用圆周角定理证明∠ADE=∠DAC得到FD=FA=5,再根据正弦的定义计算出EF=3,则AE=4,DE=8,接着证明△ADE∽△DBE,利用相似比得到BE=16,所以AB=20,然后在Rt△ABC中利用正弦定义计算出BC的长.
解:连接BD,如图,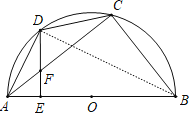
∵AB为直径,
∴∠ADB=∠ACB=90°,
∵AD=CD,
∴∠DAC=∠DCA,
而∠DCA=∠ABD,
∴∠DAC=∠ABD,
∵DE⊥AB,
∴∠ABD+∠BDE=90°,
而∠ADE+∠BDE=90°,
∴∠ABD=∠ADE,
∴∠ADE=∠DAC,
∴FD=FA=5,
在Rt△AEF中,∵sin∠CAB= ![]() ,
,
∴EF=3,
∴AE= ![]() =4,DE=5+3=8,
=4,DE=5+3=8,
∵∠ADE=∠DBE,∠AED=∠BED,
∴△ADE∽△DBE,
∴DE:BE=AE:DE,即8:BE=4:8,
∴BE=16,
∴AB=4+16=20,
在Rt△ABC中,∵sin∠CAB= ![]() ,
,
∴BC=20×![]() =12.
=12.
故选:C.

练习册系列答案
相关题目