题目内容
【题目】我市高新区某企业接到一批产品的生产任务，按要求必须在14天内完成．已知每件产品的售价为60元．工人甲第x天生产的产品数量为y件，y与x满足如下关系：
．
（1）工人甲第几天生产的产品数量为60件？
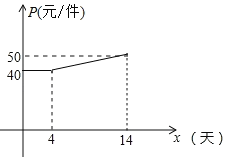
（2）设第x天生产的产品成本为P元/件，P与x的函数关系图象如图，工人甲第x天创造的利润为W元，求W与x的函数关系式，第几天时，利润最大，最大利润是多少？
【答案】（1）工人甲第10天生产的产品数量为60件；（2）
，第11天时，利润最大，最大利润是845元．
【解析】
（1）将
分别代入
和
，根据x的取值范围选择合适的解即可；
（2）由函数图象，分段求出P与x的函数关系，再由总利润=每件的利润
产品数量可得W与x的函数关系式，结合关系式和x的取值范围确定利润的最大值即可.
解：（1）根据题意，得：
∵若8x=60，得：x=
＞4，不符合题意；
∴5x+10=60，
解得：x=10，
答：工人甲第10天生产的产品数量为60件；
（2）由函数图象知，当0≤x≤4时，P=40，
当4＜x≤14时，设P=kx+b，
将（4，40）、（14，50）代入，得：
，
解得：
，∴P=x+36；
①当0≤x≤4时，W=（60﹣40）8x=160x．
∵W随x的增大而增大，∴当x=4时，W最大=640元；
②当4＜x≤14时，W=（60﹣x﹣36）（5x+10）=﹣5x2+110x+240=﹣5（x﹣11）2+845，∴当x=11时，W最大=845．
∵845＞600，∴当x=11时，W取得最大值，845元，
答：第11天时，利润最大，最大利润是845元．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
