题目内容
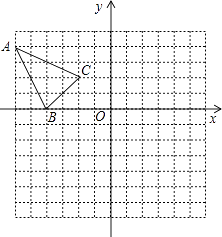
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
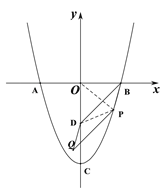
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
【答案】(1)①抛物线解析式为y=x2﹣4;②0<S四边形BDQP≤![]() ;(2)
;(2)![]() 的值与a,c无关,比值为1.
的值与a,c无关,比值为1.
【解析】试题分析:(1)①把 A(-2,0),C(0,-4)代入![]() ,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(
,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(![]() ,
, ![]() ),因A(-2,0),对称轴为
),因A(-2,0),对称轴为![]() 轴,可得B(2,0),即可得
轴,可得B(2,0),即可得![]()
![]()
![]() ,再由点P在第四象限运动,可得x单位取值范围
,再由点P在第四象限运动,可得x单位取值范围![]() ,由抛物线的图象即可得△BDP的取值范围为
,由抛物线的图象即可得△BDP的取值范围为![]() ,因
,因![]() 即可得平行四边形BDQP面积的取值范围为
即可得平行四边形BDQP面积的取值范围为![]() ;(2)过点P作PG⊥AB,设A(
;(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() ),由PG∥
),由PG∥![]() 轴,根据相似三角形的判定方法可得
轴,根据相似三角形的判定方法可得![]() ,
, ![]() ,再由相似三角形的性质可得
,再由相似三角形的性质可得![]() ,
, ![]() ,代入数值可得
,代入数值可得![]() ,
, ![]() ,把这两个式子相加可得
,把这两个式子相加可得![]() ,令
,令![]() ,即可得
,即可得![]() ,
, ![]() ,所以
,所以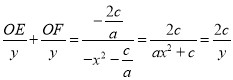 ,即
,即![]() ,所以
,所以![]() ,即可得
,即可得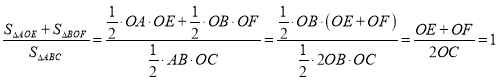
所以可得结论![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.
试题解析:
(1)①![]()
②连接DB、OP,设P(![]() ,
, ![]() )
)
∵A(-2,0),对称轴为![]() 轴
轴
∴B(2,0)
∴![]()
![]()
![]()
![]()
∵点P在第四象限运动
∴![]()
∴由抛物线的图象可得: ![]()
∵![]() ∴
∴![]()
(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() )
)

∴PG∥![]() 轴
轴
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵当![]() 时,∴
时,∴![]() ,即
,即![]() ,
, ![]()
∴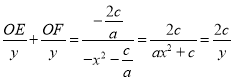
∴![]() ∴
∴![]()
∴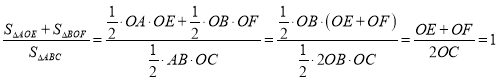
∴![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.

【题目】学校准备设计一款女生校服,对全校女生喜欢的颜色进行了问卷调查,统计如下表所示:
颜色 | 黄色 | 绿色 | 白色 | 紫色 | 红色 |
学生人数 | 100 | 180 | 220 | 80 | 750 |
学校决定采用红色,可用来解释这一现象的统计知识是( )
A. 平均 B. 中位数 C. 众数 D. 方差