题目内容
【题目】正方形A1B1C1O , A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点
C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点Bn的坐标是 .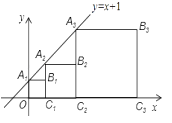
【答案】( ![]() -1,
-1, ![]() )
)
【解析】设直线y=x+1与x轴的交点为D,∵直线y=x+1,当x=0时,y=1,则A1(0,1),当y=0时,x=-1,则D(-1,0)
∴OA1=1,OD=1,
∴∠ODA1=45°,OC1
∴∠A2A1B1=45°,
∴A2B1=A1B1=1,
∴A2C1=2=21 ,
在正方形A1B1C1O中,
B1C1=OA1=1,
OC1=A1B1=1,
则B1(1,1);
A2C1=2,OC2=1+2=3,
则B2(3,2)
∴Bn的横坐标为An+1的横坐标,纵坐标为An的纵坐标
又An的横坐标数列为An=2n-1-1,所以纵坐标为2n-1 ,
∴Bn的坐标为[A(n+1)的横坐标,An的纵坐标]=(2n-1,2n-1).
观察点Bn的横坐标,纵坐标,可发现Bn的横坐标为An+1的横坐标,纵坐标为An的纵坐标.分别找出An+1的横坐标,纵坐标为An的纵坐标的规律.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目