题目内容
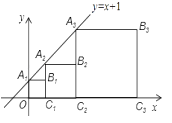
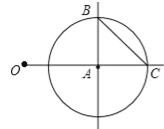
【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC
(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于![]() ;
;
②连OD,在OD上画出点P,使OP得长等于![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
【答案】(1)![]() ;(2)①A;BC;②答案见解析.
;(2)①A;BC;②答案见解析.
【解析】(1)在Rt△BAC中,AB=AC=1,∠BAC=90°,∴BC=![]() =
=![]() .故答案为:
.故答案为:![]() .
.
(2)①在Rt△OAD中,OA=2,OD=![]() ,∠OAD=90°,∴AD=
,∠OAD=90°,∴AD=![]() =
=![]() =BC,∴以点A为圆心,以线段BC的长为半径画弧,与射线BA交于点D,使线段OD的长等于
=BC,∴以点A为圆心,以线段BC的长为半径画弧,与射线BA交于点D,使线段OD的长等于![]() .
.
依此画出图形,如图1所示.
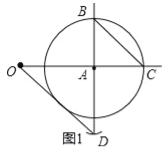
故答案为:A;BC.
②∵OD=![]() ,OP=
,OP=![]() ,OC=OA+AC=3,OA=2,∴
,OC=OA+AC=3,OA=2,∴![]() .
.
故作法如下:
连接CD,过点A作AP∥CD交OD于点P,P点即是所要找的点.
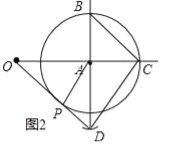
依此画出图形,如图2所示.

练习册系列答案
相关题目
【题目】个旧二中八年级9个班的全体同学参加学校第三届“青春之歌”歌咏比赛,班级的得分情况如下表:
班级(个) | 2 | 3 | 2 | 1 |
分数(分) | 92 | 94 | 96 | 97 |
那么这9个班级所得分数的众数和中位数分别是( )
A.97,92B.94,94C.94,95D.96,94