题目内容
如图,已知等腰梯形ABCD,AD∥BC,∠D=120°

(1)用直尺和圆规作出∠BAD的平分线AE,交BC于点 ,(保留作图痕迹,不要求写作法);
,(保留作图痕迹,不要求写作法);
(2)求证:四边形AECD是平行四边形。

(1)用直尺和圆规作出∠BAD的平分线AE,交BC于点
 ,(保留作图痕迹,不要求写作法);
,(保留作图痕迹,不要求写作法);(2)求证:四边形AECD是平行四边形。
(1) (2)可证明对边平行且相等。
(2)可证明对边平行且相等。
 (2)可证明对边平行且相等。
(2)可证明对边平行且相等。试题分析:(1)
 以A为圆心,以AB为半径作圆画弧交于B点和AD线段上。以两弧所得交点分别为圆心以相当半径在上下画弧,得到两个交叉,用直尺连结交叉点,得到∠BAD平分线。
以A为圆心,以AB为半径作圆画弧交于B点和AD线段上。以两弧所得交点分别为圆心以相当半径在上下画弧,得到两个交叉,用直尺连结交叉点,得到∠BAD平分线。
(2)证明:∵四边形ABCD是等腰梯形
∴AD∥BC, ∠BAD =∠D =120°
∵AE平分∠BAD
∴∠EAD=60°
∴∠EAD+∠D=180°
∴AE∥DC,
∴四边形AECD是平行四边形
点评:本题难度中等,主要考查学生尺规作图能力和平行四边形判定知识点的掌握。为中考常考题型,学生要牢固掌握作图技巧。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



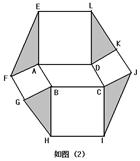

 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12


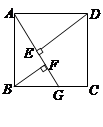
 的平分线
的平分线 交边
交边 于
于 ,
, 的平分线
的平分线 交
交 ,交
,交 .若AB=3,BC=5,求EG的长。
.若AB=3,BC=5,求EG的长。
