题目内容
已知,如图所示,正方形ABCD,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN,求证:EF=MN.




通过四边形 EFGD 为平行四边形得MN=EF
试题分析:作 DG∥EF 交 BC 于 G ,作CH∥MN 交 AB 于 H.
∵ CH∥MN , DG∥EF , FE ⊥ MN
∴ CH ⊥ DG ,又∵ DC ⊥ BC
∴∠BCH=∠CDG ,∵ BC="CD" ,∠ HBC=∠GCD
∴△DCG 按顺时针旋转 90°后再向左平移 .
BC 的长可与△ CBH 重合 .
∴ CH="DG" ,又∵ AD∥BC,DG∥EF
∴四边形 EFGD 为平行四边形,∴ EF="DG" ,
同理 CH="MN" ,∴ MN=EF
点评:本题考查平行四边形的判定,掌握平行四边形的判定方法,会判断一个四边形是平行四边形

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目



 ,(保留作图痕迹,不要求写作法);
,(保留作图痕迹,不要求写作法);




 ,
,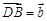 ,则用向量
,则用向量 、
、 表示向量
表示向量 为 .
为 .
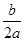 时,二次函数y=ax+bx+c(a≠o)有最小(大)值
时,二次函数y=ax+bx+c(a≠o)有最小(大)值 )
)