题目内容
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AC于点O.

(1)△ABF≌△CAE;
(2)HD平分∠AHC吗?为什么?

(1)△ABF≌△CAE;
(2)HD平分∠AHC吗?为什么?
(1)根据菱形的性质可得AB=BC,再结合AB=AC可得△ABC为等边三角形,即可得到∠B=∠CAB=60°,再结合AE=BF,AB=AC即可证得结论;(2)平分
试题分析:(1)根据菱形的性质可得AB=BC,再结合AB=AC可得△ABC为等边三角形,即可得到∠B=∠CAB=60°,再结合AE=BF,AB=AC即可证得结论;
(2)过点D作DG⊥CH于点G,作DK⊥FA交FA的延长线于点K,由△ABF≌△CAE.可得∠BAF=∠CAE,即可得到∠CAE+∠CAF=60°,则∠AHC=120°,由∠ADC=60°,可得∠HAD+∠HCD=180°,从而可得∠HCD=∠KAD,即可证得△ADK≌△CDG,再结合DG⊥CH,DK⊥FA即可得到结论.
(1)∵ABCD为菱形,
∴AB=BC.
∵AB=AC,
∴△ABC为等边三角形.
∴∠B=∠CAB=60°.
又∵AE=BF,AB=AC,
∴△ABF≌△CAE;
(2)过点D作DG⊥CH于点G,作DK⊥FA交FA的延长线于点K,
∵△ABF≌△CAE.
∴∠BAF=∠CAE,
∵∠BAF+∠CAF=60°,
∴∠CAE+∠CAF=60°,
∴∠AHC=120°,
∵∠ADC=60°,
∴∠HAD+∠HCD=180°,
∵∠HAD+∠KAD=180°,
∴∠HCD=∠KAD,
∵AD=CD,∠DGC=∠AKD=90°,
∴△ADK≌△CDG,
∴DK=DG,
∵DG⊥CH,DK⊥FA,
∴HD平分∠AHC.
点评:此类问题知识点较多,综合性较强,是中考常见题,一般难度不大.

练习册系列答案
相关题目
 ,则菱形ABCD的面积是__________
,则菱形ABCD的面积是__________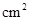 .
.
 ,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③
,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③ ;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。

 ,(保留作图痕迹,不要求写作法);
,(保留作图痕迹,不要求写作法);




