题目内容
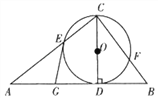
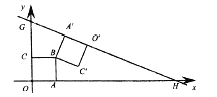
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,边长为2的正方形
两点,边长为2的正方形![]() 的边
的边![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,点
轴上,点![]() 在第一象限,正方形
在第一象限,正方形![]() 绕点
绕点![]() 逆时针旋转,
逆时针旋转,![]() 的对应边
的对应边![]() 恰好落在直线
恰好落在直线![]() 上,则
上,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C. 5D. 6
C. 5D. 6
【答案】C
【解析】
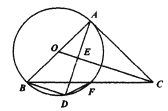
连接GB并延长交x轴于点D,过点D作DM⊥GH于点M..利用角平分线的判定定理易证GD平分∠OGH,再根据角平分线的性质证明DO=DM,根据直线解析式解得OG=b=MG,OH=![]() b,由勾股定理得GH=
b,由勾股定理得GH=![]() b,因为CB∥OD,所以△GCB∽△GOD,根据相似三角形的性质可得:
b,因为CB∥OD,所以△GCB∽△GOD,根据相似三角形的性质可得:![]() ,即
,即![]() ,解得OD=
,解得OD=![]() =DM, 再证明△HDM∽△HGO,所以
=DM, 再证明△HDM∽△HGO,所以![]() ,即
,即 ,解得:b1=0(舍去),b2=5。
,解得:b1=0(舍去),b2=5。
解:连接GB并延长交x轴于点D,过点D作DM⊥GH于点M..
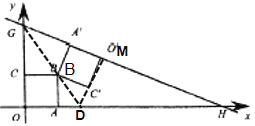
∵BC⊥OG于点C,BA′⊥GH于点A′,BC=BA′=2,DO⊥OG于点O,DM⊥GH于点M,(易证M与O′重合)
∴GD平分∠OGH,DO=DM,
又∵GD=GD,
∴Rt△GOD≌Rt△GMD(HL)
∴OG=MG
∵直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,
两点,
∴OG=b=MG,OH=![]() b,由勾股定理得GH=
b,由勾股定理得GH=![]() b,
b,
∴MH=GH- MG=![]() b,
b,
∵CB∥OD,
∴△GCB∽△GOD
∴![]() ,即
,即![]() ,解得OD=
,解得OD=![]() =DM,
=DM,
易证△HDM∽△HGO,
∴![]() ,即
,即 ,解得:b1=0(舍去),b2=5,
,解得:b1=0(舍去),b2=5,
故选:C.

练习册系列答案
相关题目
【题目】某数学兴趣小组对函数y=![]() 的图象和性质进行探究,他们用描点法画此函数图象时,先列表如下
的图象和性质进行探究,他们用描点法画此函数图象时,先列表如下
(1)请补全此表;
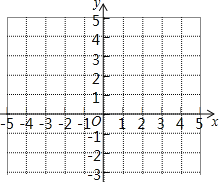
(2)根据表中数据,在如图坐标系中画出该函数的图象;
(3)请写出此函数图象不同方面的三个性质;
(4)若点(m,y1),(2,y2)都在此函数图象上,且y1≤y2,求m的取值范围
x | …… | _____ | ____ | _____ | _____ | 0 | 1 | 2 | 3 | 4 | …… |
y | …… | _____ | ____ | _____ | _____ | 4 | 2 |
|
|
|