题目内容
【题目】如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.
【答案】![]() 或
或![]()
【解析】
因为点A,B的对应点G,F分别在直线AD与BC上,所以分两种情况讨论, 当∠EFD=90°时,证明△EFN∽△FDC,设CD=5a,根据比例式表示出CN,BN即可;当∠EDF=90°时,证明△FCD∽△DCB,设CD=3a, 根据比例式表示出CN,BN即可.
解:分两种情况:
当∠EFD=90°时,如下图,
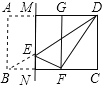
∵∠EFN=∠C=90°,易证∠EFN=∠FDC,
∴△EFN∽△FDC,
设CD=5a,由题可知,CF=3a,
∴![]() ,∴BC=
,∴BC=![]() ,
,
∴BN=NF=![]() ,即
,即![]()
当∠EDF=90°时,如下图,
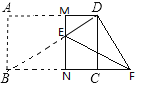
同理易证:△FCD∽△DCB,
设CD=3a,则BC=5a,CF=![]()
∴BF=5a+![]() ,
,
∴BN=![]() ,NC=
,NC=![]() ,
,
∴![]()
综上, CN:BN的值为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目