Question

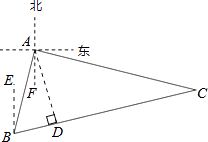
【题目】如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．

（1）求点C与点A的距离（精确到1km）；
（2）确定点C相对于点A的方向．
（参考数据： ≈1.414， ≈1.732）

Answer 1

【答案】
（1）

解：如右图，过点A作AD⊥BC于点D，∠ABE=∠BAF=15°，

由图得，∠ABC=∠EBC﹣∠ABE=∠EBC﹣∠BAF=75°﹣15°=60°，

在Rt△ABD中，∵∠ABC=60°，AB=100，

∴BD=50，AD=50 ，

∴CD=BC﹣BD=200﹣50=150，

在Rt△ACD中，由勾股定理得：

AC= =100 ≈173（km）．

答：点C与点A的距离约为173km．

（2）

解：在△ABC中，∵AB2+AC2=1002+（100 ）2=40000，

BC2=2002=40000，

∴AB2+AC2=BC2，

∴∠BAC=90°，

∴∠CAF=∠BAC﹣∠BAF=90°﹣15°=75°．

答：点C位于点A的南偏东75°方向．

【解析】（1）作辅助线，构造直角三角形，解直角三角形即可；（2）利用勾股定理的逆定理，判定△ABC为直角三角形；然后根据方向角的定义，即可确定点C相对于点A的方向．
【考点精析】关于本题考查的勾股定理的概念和解直角三角形，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．