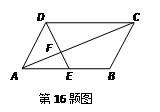题目内容
如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE = AC,以AE为一边作菱形AEFC,若菱形的面积为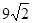 ,则正方形边长
,则正方形边长 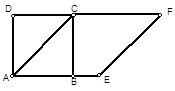
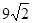 ,则正方形边长
,则正方形边长 
3
根据题意可知AC=AE,且CB⊥AE,故菱形面积S=AE?BC,且AC= 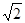 BC,根据S可求得BC的值,且BC为正方形的边长,即可解题.
BC,根据S可求得BC的值,且BC为正方形的边长,即可解题.
解:正方形边长为BC,
则对角线AC=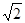 BC,
BC,
且AE=AC,
∴AE=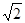 BC,
BC,
∵菱形面积S=AE?BC
∴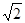 BC?BC=9
BC?BC=9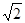 ,
,
∴BC=3.
故正方形的边长为 3.
本题考查了正方形各边长相等、各内角为直角的性质,菱形面积的计算,菱形各边长相等的性质,本题中求证AE=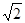 BC是解题的关键.
BC是解题的关键.
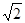 BC,根据S可求得BC的值,且BC为正方形的边长,即可解题.
BC,根据S可求得BC的值,且BC为正方形的边长,即可解题.解:正方形边长为BC,
则对角线AC=
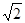 BC,
BC,且AE=AC,
∴AE=
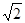 BC,
BC,∵菱形面积S=AE?BC
∴
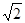 BC?BC=9
BC?BC=9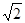 ,
,∴BC=3.
故正方形的边长为 3.
本题考查了正方形各边长相等、各内角为直角的性质,菱形面积的计算,菱形各边长相等的性质,本题中求证AE=
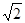 BC是解题的关键.
BC是解题的关键.
练习册系列答案
相关题目
 OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
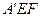 ,求△
,求△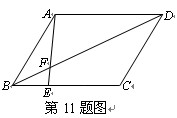

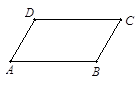
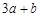 ,宽为
,宽为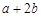 的矩形,需要
的矩形,需要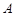 类卡片_______张,
类卡片_______张,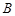 类卡片_______张,
类卡片_______张,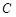 类卡片______张.
类卡片______张.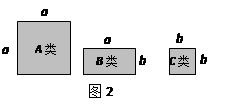
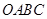 为菱形,点
为菱形,点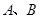 在以点
在以点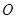 为圆心的
为圆心的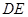 上,
上,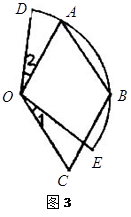
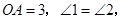 则扇形
则扇形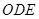 的面积为
的面积为