题目内容
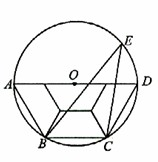
(12分)如图,直角梯形OABC的直角顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上,OA∥BC,D是BC上一点,BD= OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.

(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,将△AEF沿EF折叠,得到△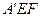 ,求△
,求△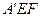 与五边形OEFBC重叠部分的面积.
与五边形OEFBC重叠部分的面积.
 OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,将△AEF沿EF折叠,得到△
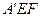 ,求△
,求△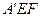 与五边形OEFBC重叠部分的面积.
与五边形OEFBC重叠部分的面积.(1)
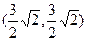
(2)
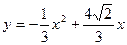
(3)
 或1或
或1或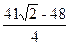
解:(1)D点的坐标是
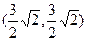 . (2分)
. (2分)(2)连结OD,如图(1),由结论(1)知:D在∠COA的平分线上,则∠DOE=∠COD=45°,
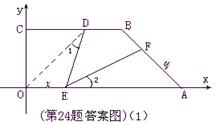
又在梯形DOAB中,∠BAO=45°,∴OD=AB=3
由三角形外角定理得:∠1=∠DEA-45°,又∠2=∠DEA-45°
∴∠1=∠2, ∴△ODE∽△AEF (4分)
∴
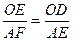 ,即:
,即: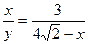
∴y与x的解析式为:
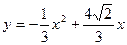 (6分)
(6分)(3)当△AEF为等腰三角形时,存在EF=AF或EF=AE或AF=AE共3种情况.
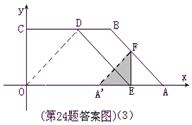
①当EF=AF时,如图(2).∠FAE=∠FEA=∠DEF=45°,∴△AEF为等腰直角三角形.
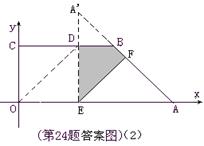
D在A’E上(A’E⊥OA),
B在A’F上(A’F⊥EF)
∴△A’EF与五边形OEFBC重叠的面积为
四边形EFBD的面积.
∵
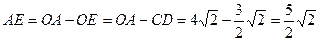
∴
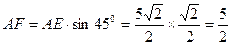
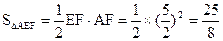
∴
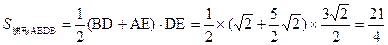
∴
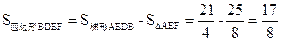 (也可用
(也可用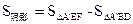 ) (8分)
) (8分)②当EF=AE时,如图(3),此时△A’EF与五边形OEFBC重叠部分面积为△A’EF面积.
∠DEF=∠EFA=45°, DE∥AB ,又DB∥EA
∴四边形DEAB是平行四边形
∴AE=DB=

∴
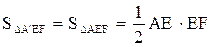
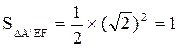 (10分)
(10分)③当AF=AE时,如图(4),四边形AEA’F为菱形且△A’EF在五边形OEFBC内.
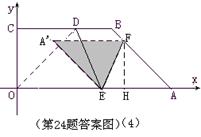
∴此时△A’EF与五边形OEFBC重叠部分面积为△A’EF面积.
由(2)知△ODE∽△AEF,则OD=OE=3
∴AE=AF=OA-OE=
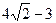
过F作FH⊥AE于H,则
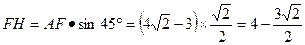
∴
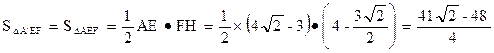
综上所述,△A’EF与五边形OEFBC重叠部分的面积为
 或1或
或1或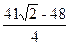 (12分)
(12分)
练习册系列答案
相关题目
 是正方形,延长
是正方形,延长 到
到 ,使
,使 ,则
,则 的度数是 ▲ °.
的度数是 ▲ °.
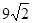 ,则正方形边长
,则正方形边长 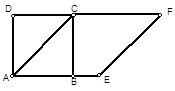
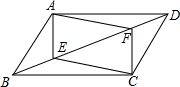
 ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等于 ㎝.
ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等于 ㎝.
 年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形
年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形 (如图
(如图 所示),
所示), ,
, 为水面,点
为水面,点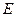 在
在 上,测得背水坡
上,测得背水坡 的长为
的长为 米,倾角
米,倾角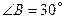 ,迎水坡
,迎水坡 上线段
上线段 的长为
的长为 米,
米, .
.
 米,参考数据
米,参考数据 );
); 天?(精确到
天?(精确到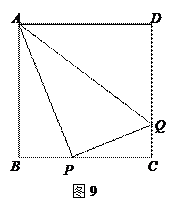
 的位置如图3所示,则
的位置如图3所示,则  的值是
的值是



 是由四个全等的等腰梯形组成,
是由四个全等的等腰梯形组成, 是
是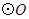 的直径,则
的直径,则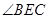 为___________度.
为___________度.