题目内容
如图,平行四边形ABCD中,AB=6,BC=4,∠A=60°,要用一块矩形铝板切割出这样的平行四边形,使废料最少,则所需铝板的面积最小应是_______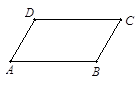

16

有两种方法可以得到这个矩形,分别计算这两种矩形的面积,找出其面积最小的一个.
方法1:过B点作AD的垂线,交DA延长线于E点;过D点作BC垂线,交BC延长线于F点.矩形BEDF为一种情形,其面积为21 ;
;
方法2:过D点作AB的垂线,交BA延长线于E点;过B点作CD垂线,交DC延长线于F点.矩形BFDE为另外一种情形,其面积16 .
.
根据以上分析,矩形面积最小为方法2,最小面积为16 .
.

解:方法1:过B点作AD的垂线,交DA延长线于E点;过D点作BC垂线,交BC延长线于F点.如图,
∵∠ABC=60°,∴∠ABE=30°,
∵AB=6,∴AE=3,BE=3 ,
,
∴矩形BEDF的面积为7×3 =21
=21 ;
;
方法2:过D点作AB的垂线,交BA延长线于E点;过B点作CD垂线,交DC延长线于F点.
如图,
∵∠ABC=60°,∴∠CBF=30°,
∵CB=4,∴CF=2,BF=2 ,
,
∴矩形BEDF的面积为8×2 =16
=16 ;
;
根据以上分析,矩形面积最小为方法2,最小面积为16 .
.
故答案为16 .
.
本题考查了面积及等级变换,根据平行四边形的形状,补充出两种不同形状的矩形,再求其面积是解此题的关键.
方法1:过B点作AD的垂线,交DA延长线于E点;过D点作BC垂线,交BC延长线于F点.矩形BEDF为一种情形,其面积为21
 ;
;方法2:过D点作AB的垂线,交BA延长线于E点;过B点作CD垂线,交DC延长线于F点.矩形BFDE为另外一种情形,其面积16
 .
.根据以上分析,矩形面积最小为方法2,最小面积为16
 .
.
解:方法1:过B点作AD的垂线,交DA延长线于E点;过D点作BC垂线,交BC延长线于F点.如图,
∵∠ABC=60°,∴∠ABE=30°,
∵AB=6,∴AE=3,BE=3
 ,
,∴矩形BEDF的面积为7×3
 =21
=21 ;
;方法2:过D点作AB的垂线,交BA延长线于E点;过B点作CD垂线,交DC延长线于F点.

如图,
∵∠ABC=60°,∴∠CBF=30°,
∵CB=4,∴CF=2,BF=2
 ,
,∴矩形BEDF的面积为8×2
 =16
=16 ;
;根据以上分析,矩形面积最小为方法2,最小面积为16
 .
.故答案为16
 .
.本题考查了面积及等级变换,根据平行四边形的形状,补充出两种不同形状的矩形,再求其面积是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 ,
, ,
, ,
, 。直角三角板含
。直角三角板含 角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若
角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F,若 是以AB为腰的等腰三角形,则CF的等于_____
是以AB为腰的等腰三角形,则CF的等于_____
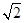 ∶1
∶1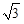 ∶1
∶1
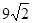 ,则正方形边长
,则正方形边长 
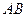 为
为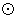
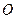 的直径,
的直径,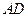 与
与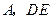 与
与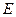 ,点
,点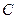 为
为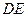 延长线上一点,且
延长线上一点,且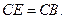
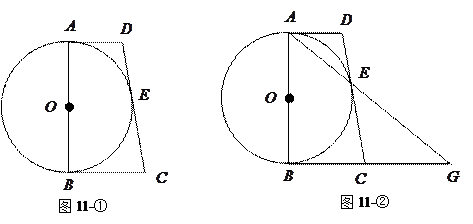
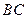 为
为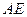 ,
,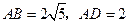 ,求线段
,求线段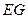 的长.
的长. 年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形
年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形 (如图
(如图 所示),
所示), ,
, 为水面,点
为水面,点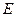 在
在 上,测得背水坡
上,测得背水坡 的长为
的长为 米,倾角
米,倾角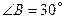 ,迎水坡
,迎水坡 上线段
上线段 的长为
的长为 米,
米, .
.
 米,参考数据
米,参考数据 );
); 天?(精确到
天?(精确到