题目内容
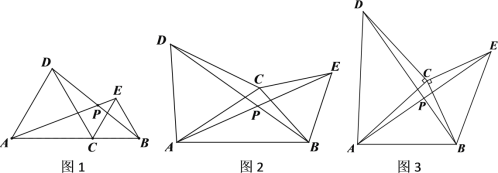
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
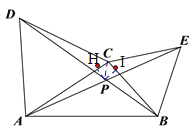
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
【答案】(1)AE=BD.∠APC=60°;(2)成立,见详解;(3)AE=BD
【解析】
(1)观察猜想:①证明△ACE≌△DCB(SAS),可得AE=BD,∠CAE=∠BDC;
②过点C向AE,BD作垂线,由三角形全等可得高相等,再根据角分线判定定理,推出PC平分∠APB,即可求出∠APC的度数;
(2)数学思考:结论成立,证明方法类似;
(3)拓展应用:证明△ACE≌△DCB(SAS),即可得AE=BD.
解:(1)观察猜想:结论:AE=BD.∠APC=60°.
理由: ①∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD;
②由①得∠EAC=∠BDC,
∵∠AOC=∠DOP,
∴∠APB=∠AOC+∠EAC=180°-60°= 120°.
过过点C向AE,BD作垂线交于点F与G
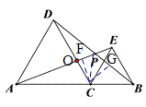
∵由①知△ACE≌△DCB
∴CF=CG
∴CP为∠APB的角平分线
∴∠APC=![]() 60°;
60°;
(2)数学思考:结论仍然成立.
①∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD;
②由①得∠AEC=∠DBC,
∴∠CEA+∠PEB=∠CBD+∠PEB=60°,
∴∠APB=∠CBD+∠CBE+∠PEB=120°.
过过点P向AC,BC作垂线交于点H与I
∵由①知△ACE≌△DCB
∴PH=PI
∴CP为∠APB的角平分线
∴∠APC=![]() 60°;
60°;
(3)∵△ADC,△ECB都是等腰直角三角形,
∴CA=CD,∠ACD=∠ECB=90°,CE=CB,
∴∠ACB+∠BCE=∠ACB+∠ACD
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案