题目内容
【题目】如图,在⊙O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F 
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
【答案】
(1)解:四边形ABCD是矩形.理由如下:
∵AC与BD是圆的直径,
∴∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,
∴四边形ABCD是矩形;
(2)解:证明:∵BO=CO,
又∵BE⊥AC于E,CF⊥BD于F,
∴∠BEO=∠CFO=90°.
在△BOE和△COF中, 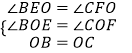 ,
,
∴△BOE≌△COF(AAS).
∴BE=CF.
【解析】(1)由圆周角定理得出∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,即可得出四边形ABCD是矩形;(2)由AAS证明△BOE≌△COF,得出对应边相等即可.
【考点精析】根据题目的已知条件,利用矩形的判定方法和圆周角定理的相关知识可以得到问题的答案,需要掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目