题目内容
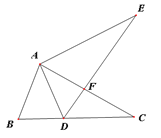
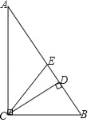
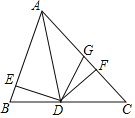
【题目】如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
(1)根据角平分线的性质可得出DE=DF,结论(1)正确;
(2)由DE=DF、∠BED=∠GFD、BD=GD可证出△BDE≌△GDF(HL),根据全等三角形的性质可得出∠B=∠DGF,结论(2)正确;
(3)利用全等三角形的判定定理AAS可证出△ADE≌△ADF,由此可得出AE=AF,根据△BDE≌△GDF可得出BE=GF,结合AB=AE+EB即可得出AB=AF+FG,结论(3)不正确;
(4)根据全等三角形的性质可得出S△ADE=S△ADF、S△BDE=S△GDF,结合S△ABD=S△ADE+S△BDE=50、S△ADG=S△ADF-S△GDF=38可求出△DFG的面积是6,结论(4)不正确.综上即可得出结论.
(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,结论(1)正确;
(2)在△BDE和△GDF中,![]() ,
,![]()
∴△BDE≌△GDF(HL),
∴∠B=∠DGF,结论(2)正确;
(3)在△ADE和△ADF中,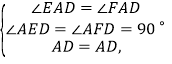
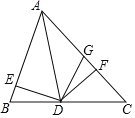
∴△ADE≌△ADF(AAS),
∴AE=AF.
∵△BDE≌△GDF,
∴BE=GF,
∴AB=AE+EB=AF+FG,结论(3)不正确;
(4)∵△ADE≌△ADF,△BDE≌△GDF,
∴![]()
∵![]()
∴![]() ,结论(4)不正确。
,结论(4)不正确。
综上所述:正确的结论有(1)(2).
故选:B.

【题目】下表中有两种移动电话计费方式:
月使用费 | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.20 | 免费 |
方式二 | 100 | 380 | 0.25 | 免费 |
(月使用费固定收;主叫不超过限定的时间不再收费,主叫超过限定时间的部分加收超时费;被叫免费)
(1)若张聪某月主叫通话时间为200分钟,则他按方式一计费需____元,按方式二计费需____
元;李华某月按方式二计费需107元,则李华该月主叫通话时间为_____分钟;
(2)是否存在某主叫通话时间![]() (分钟),按方式一和方式二的计费相等?若存在,请求出
(分钟),按方式一和方式二的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)直接写出当月主叫通话时间![]() (分钟)满足什么条件时,选择方式一省钱。
(分钟)满足什么条件时,选择方式一省钱。