题目内容
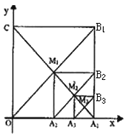
【题目】如图 ,在平面直角坐标系中,边长为 1 的正方形OA1B1C 的对角线 A1C 和OB1 交于点 M1,以 M1A1为对角线作第二个正方形 A2A1B2M1对角线 A1M1和 A2 B2 交于点 M 2 ;以 M 2 A1 为对角线作第三个正方形 A3 A1B3M 2,对角线 A1M 2 和 A3 B3 交于点 M 3 ;…,依此类推,那么 M 1 的坐标为_____;这样作的第 n 个正方形的对角线交点 Mn 的坐标为_____.
【答案】(![]() ) (1-
) (1-![]()
![]()
【解析】
根据正方形的性质得到OM1=M1A1,∠OM1A1=90°,设OM1=M1A1=x,由勾股定理得到方程x![]() +x
+x![]() =1
=1![]() ,解方程求出x的值,同理可以求出其它正方形的边长,进而得到M1的坐标,M2的坐标,…,依此类推可求出第n个正方形对角线交点M
,解方程求出x的值,同理可以求出其它正方形的边长,进而得到M1的坐标,M2的坐标,…,依此类推可求出第n个正方形对角线交点M![]() 的坐标.
的坐标.
解:∵正方形的边长为1,
则正方形四个顶点坐标为O(0,0),C(0,1),B1 (1,1),A1 (1,0),
在正方形OA1B1C中,
∴OM1=M1A1,∠OM1A1=90,
设OM1=M1A1=x,
由勾股定理得:x![]() +x
+x![]() =1
=1![]() ,
,
解得:x=![]() ,
,
同理可求出OA2=A2M1=![]() ,A2M2=
,A2M2=![]() ,A2A
,A2A![]() ,…,
,…,
根据正方形对角线定理得M1的坐标为(1![]() ,
,![]() );
);
同理得M2的坐标为(1![]() ,
,![]() );
);
M![]() 的坐标为(1
的坐标为(1![]() ,
,![]() ),
),
依此类推:M![]() 坐标为(1-
坐标为(1-![]()
![]()
故答案为: (![]() ) (1-
) (1-![]()
![]()

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目