题目内容
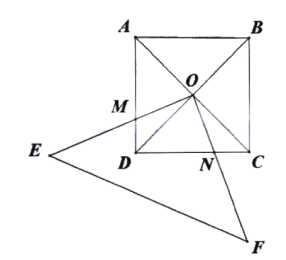
【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
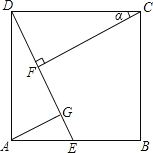
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
【答案】(1)证明见解析
(2)sinα=![]() 。
。
【解析】
试题分析:(1)由正方形的性质得AD=DC,∠ADC=90°,根据垂直的定义求出∠CFD=∠CFG=90°,再根据两直线平行,内错角相等求出∠AGD=∠CFG=90°,从而得到∠AGD=∠CFD,再根据同角的余角相等求∠ADG=∠DCF,然后利用“角角边”证明△DCF和△ADG全等即可。
(2)设正方形ABCD的边长为2a,表示出AE,再利用勾股定理列式求出DE,然后根据锐角的正弦等于对边比斜边求出∠ADG的正弦,即为α的正弦。
解:(1)证明:在正方形ABCD中,AD=DC,∠ADC=90°,
∵CF⊥DE,∴∠CFD=∠CFG=90°。
∵AG∥CF,∴∠AGD=∠CFG=90°。∴∠AGD=∠CFD。
又∵∠ADG+∠CDE=∠ADC=90°,∠DCF+∠CDE=90°,∴∠ADG=∠DCF。
∵在△DCF和△ADG中,∠AGD=∠CFD,∠ADG=∠DCF,AD=DC,
∴△DCF≌△ADG(AAS)。
(2)设正方形ABCD的边长为2a,
∵点E是AB的中点,∴AE=![]() ×2a=a。
×2a=a。
在Rt△ADE中,![]() ,
,
∴![]() 。
。
∵∠ADG=∠DCF=α,∴sinα=![]() 。
。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?