题目内容
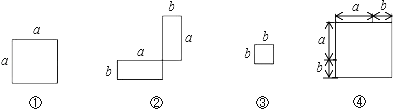
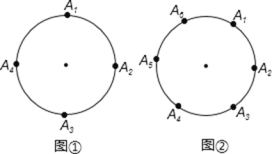
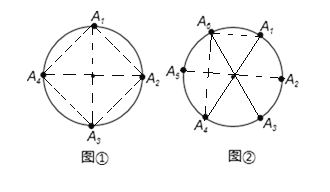
【题目】如图①,如果 A1、A2、A3、A4 把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形4个;如图②,如果A1、A2、A3、A4、A5、A6 把圆周六等分,则以A1、A2、A3、A4、A5、A6 为点的直角三角形有 12 个;如果 A1、A2、A3、……A2n 把圆周 2n 等分,则以 A1、A2、A3、…A2n为顶点的直角三角形有__________个,
【答案】2n(n-1)
【解析】
根据圆周角定理找到直径所对的圆周角是直角,然后由一条直径所对的直角数来寻找规律.
![]() 解:由圆周角定理知,直径所对的圆周角是直角.
解:由圆周角定理知,直径所对的圆周角是直角.
∴当A1、A2、A3、A4把圆周四等分时,该圆中的直径有A1A3,A2A4两条,
∴①当以A1A3为直径时,有两个直角三角形;
②当以A2A4为直径时,有两个直角三角形;
∴如果A1、A2、A3、A4把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形有(4÷2)×(4-2)=4个;
当A1、A2、A3、A4、A5、A6把圆周六等分,则以A1、A2、A3、A4、A5、A6为顶点的直角三角形有(6÷2)×(6-2)=12个;
当A1、A2、A3、…A2n把圆周2n等分,则以A1、A2、A3、…A2n为顶点的直角三角形有(2n÷2)×(2n-2)=2n(n-1)个.
故答案是:2n(n-1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目