题目内容
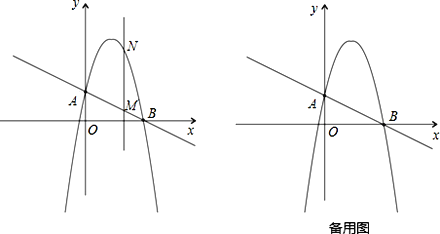
【题目】将一矩形纸片OABC 放在平面直角坐标系中, O(0,0) , A(6,0) , C(0,3) .动点Q 从点O 出发以每秒 1 个单位长的速度沿OC 向终点C 运动,运动![]() 秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
(1)用含t 的代数式表示OP,OQ ;
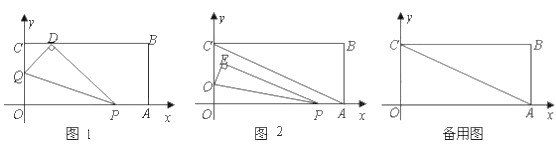
(2)当t 1时,如图 1,将△OPQ 沿 PQ 翻折,点O 恰好落在CB 边上的点 D 处,求点 D 的坐标;
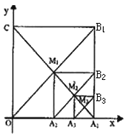
(3)连结 AC ,将△OPQ 沿 PQ 翻折,得到△EPQ ,如图 2.问: PQ 与 AC 能否平行? PE 与 AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.
【答案】(1) OP 6 t , OQ t ![]() (2)D(1,3);(3)① PQ 能与 AC 平行,t
(2)D(1,3);(3)① PQ 能与 AC 平行,t ![]() ,② PE 不能与 AC 垂直,理由见解析.
,② PE 不能与 AC 垂直,理由见解析.
【解析】
(1)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据P点与Q点的运动速度与运动时间即可用含t的代数式表示OP,OQ;
(2)由翻折的性质可知:△OPQ≌△DPQ,进而可得:DQ=OQ,然后由t=1时,DQ=OQ=![]() ,CQ=OCOQ=
,CQ=OCOQ=![]() ,然后利用勾股定理可求CD的值,进而可求点D的坐标;
,然后利用勾股定理可求CD的值,进而可求点D的坐标;
(3)① PQ 能与 AC 平行。若 PQ ∥ AC ,得到![]() ,t
,t ![]() ;② PE 不能与 AC 垂直。若 PE AC ,延长QE 交OA 于 F,得到
;② PE 不能与 AC 垂直。若 PE AC ,延长QE 交OA 于 F,得到![]() ,t 3.45 ,即可解答
,t 3.45 ,即可解答
(1)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点Q从O点以每秒1个单位长的速度沿OC向终点C运动,运动23秒时,动点P从点A出发以相等的速度沿AO向终点O运动.
∴当点P的运动时间为t(秒)时,
AP=t,OQ t ![]() ,
,
则OP=OAAP=6t;
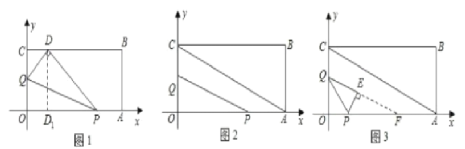
(2)当t 1时,过 D 点作 DD1 OA ,交OA 于 D1 ,如图 1,
则 DQ QO=![]() , QC
, QC ![]() ,
,
CD 1 , D(1,3)
(3)① PQ 能与 AC 平行.若 PQ ∥ AC ,如图 2,
则![]() ,
,
即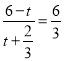 ,
,
t ![]() ,而0 ≤ t ≤
,而0 ≤ t ≤![]() ,
,
t ![]() ,
,
② PE 不能与 AC 垂直。
若 PE AC ,延长QE 交OA 于 F ,如图 3,
QF ![]() ,
,
EF QF QE QF OQ ![]() (t
(t ![]() - (t
- (t ![]() =(
=(![]()
![]()
又Rt△EPF ∽ Rt△OCA ,
![]() ,
,
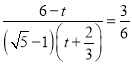
t 3.45 .
而0 ≤ t ≤![]() .
.
∴ t 不存在.

【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?