题目内容
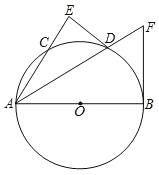
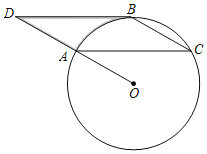
【题目】如图,AB为⊙O的直径,C为圆外一点,AC交⊙O于点D,BC2=CDCA,弦ED=弦BD,BE交AC于F.

(1)求证:BC为⊙O切线;
(2)判断△BCF的形状并说明理由;
(3)已知BC=15,CD=9,求tan∠ADE的值.
【答案】(1)证明见解析;(2)△BCF为等腰三角形.证明见解析;(3)![]()
【解析】
(1)由BC2=CDCA,根据三角形相似的判定得到△CBD∽△CAB,根据三角形相似的性质得到∠CBD=∠BAC,而AB为⊙O的直径,根据圆周角定理的推论得∠ADB=90°,易证得∠ABD+∠CBD=90°,根据切线的判定即可得到答案;
(2)由![]() ,根据圆周角定理得∠DAE=∠BAC,由(1)得∠BAC=∠CBD,则∠CBD=∠DAE,根据同弧所对的圆周角相等得∠DAE=∠DBF,所以∠DBF=∠CBD,而∠BDF=90°,根据等腰三角形三线的判定即可得到△BCF为等腰三角形;
,根据圆周角定理得∠DAE=∠BAC,由(1)得∠BAC=∠CBD,则∠CBD=∠DAE,根据同弧所对的圆周角相等得∠DAE=∠DBF,所以∠DBF=∠CBD,而∠BDF=90°,根据等腰三角形三线的判定即可得到△BCF为等腰三角形;
(3)由BC2=CDCA,BC=15,CD=9,可计算出CA=25,根据等腰三角形的性质有BF=BC=15,DF=DC=9,利用勾股定理计算出BD=12,得到AF=7,再根据等积可求出AE=![]() ,然后利用Rt△AEF∽Rt△BDF,通过相似比可计算出EF,则可得到BE,而∠ADE=∠ABE,最后利用三角函数的性质可计算出tan∠ADE的值.
,然后利用Rt△AEF∽Rt△BDF,通过相似比可计算出EF,则可得到BE,而∠ADE=∠ABE,最后利用三角函数的性质可计算出tan∠ADE的值.
(1)证明:∵BC2=CDCA,
∴BC:CA=CD:BC,
∵∠C=∠C,
∴△CBD∽△CAB,
∴∠CBD=∠BAC,
又∵AB为⊙O的直径,
∴∠ADB=90°,即∠BAC+∠ABD=90°,
∴∠ABD+∠CBD=90°,即AB⊥BC,
∴BC为⊙O切线;
(2)△BCF为等腰三角形.证明如下:
∵![]() ,
,
∴∠DAE=∠BAC,
又∵△CBD∽△CAB,
∴∠BAC=∠CBD,
∴∠CBD=∠DAE,
∵∠DAE=∠DBF,
∴∠DBF=∠CBD,
∵∠BDF=90°,
∴∠DBC=∠BDF=90°
∵BD=BD
∴△BDF≌△BDC
∴BF=BC
∴△BCF为等腰三角形;
(3)解:∵BC2=CDCA,BC=15,CD=9,
∴CA=25,BF=BC=15,DF=DC=9,
∴BD=![]() =12,
=12,
∴AF=25-18=7,
∴S△ABF=![]() AEBF=
AEBF=![]() AFBD,
AFBD,
∴AE=![]() ,
,
易证Rt△AEF∽Rt△BDF,
∴EF:DF=AF:BF,即EF:9=7:15,
∴EF=![]() ,
,
∴BE=15+![]() =
=![]() ,
,
∵∠ADE=∠ABE,
∴tan∠ADE=tan∠ABE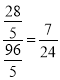 .
.

 阅读快车系列答案
阅读快车系列答案