题目内容
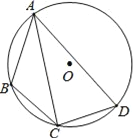
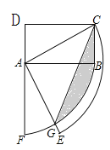
【题目】如图，矩形ABCD中，AD=1，CD=
，连接AC，将线段AC、AB分别绕点A顺时针旋转90°至AE、AF，线段AE与弧BF交于点G，连接CG，则图中阴影部分面积为__.
【答案】
﹣
【解析】
由勾股定理得到AC=2，由三角函数的定义得到∠CAB=30°，根据旋转的性质得到∠CAE=∠BAF=90°，求得∠BAG=60°，然后根据图形的面积即可求得．
在矩形ABCD中，
∵AD=1，CD=
，
∵AC=2，tan∠CAB= 
，
∴∠CAB=30°，
∵线段AC、AB分别绕点A顺时针旋转90°至AE、AF，
∴∠CAE=∠BAF=90°，
∴∠BAG=60°，
∵AG=AB=，
∴阴影部分面积=S△ABC+S扇形ABG-S△ACG
．
故答案为：﹣．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】滴滴快车是一种便捷的出行工具，某地的计价规则如下表：
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 2元/公里 |
| 1元/公里 |
注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为：行车里程7公里以内（含7公里）不收远途费，超过7公里的，超出部分每公里收1元． | |||
小李与小张分别从不同地点，各自同时乘坐滴滴快车，到同一地点相见，已知到达约定地点时他们的实际行车里程分别为7公里与9公里，两人付给滴滴快车的乘车费相同．其中一人先到达约定地点，他等候另一人的时间等于他自己实际乘车时间，且恰好是另一人实际乘车时间的一半，则小李的乘车费为______元．
