题目内容
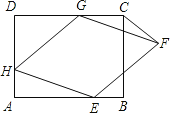
【题目】如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上,AG=CH,直线GH绕点O逆时针旋转α角,与边AB、CD分别相交于点E、F(点E不与点A、B重合).
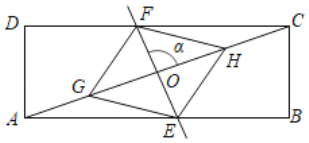
(1)求证:四边形EHFG是平行四边形;
(2)若∠α=90°,AB=9,AD=3,求AE的长.
【答案】(1)详见解析;(2)AE=5.
【解析】
(1)由“ASA”可证△COF≌△AOE,可得EO=FO,且GO=HO,可证四边形EHFG是平行四边形;
(2)由题意可得EF垂直平分AC,可得AE=CE,由勾股定理可求AE的长.
证明:(1)∵对角线AC的中点为O
∴AO=CO,且AG=CH
∴GO=HO
∵四边形ABCD是矩形
∴AD=BC,CD=AB,CD∥AB
∴∠DCA=∠CAB,且CO=AO,∠FOC=∠EOA
∴△COF≌△AOE(ASA)
∴FO=EO,且GO=HO
∴四边形EHFG是平行四边形;
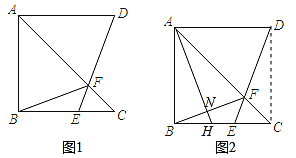
(2)如图,连接CE
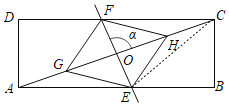
∵∠α=90°,
∴EF⊥AC,且AO=CO
∴EF是AC的垂直平分线,
∴AE=CE,
在Rt△BCE中,CE2=BC2+BE2,
∴AE2=(9﹣AE)2+9,
∴AE=5

练习册系列答案
相关题目