Question

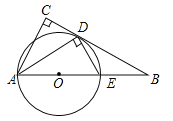
【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径．

（1）判断BC与⊙O的位置关系，并证明你的结论；

（2）求证：△ABD∽△DBE；

（3）若cosB=，AE=4，求CD．

Answer 1

【答案】（1）BC与⊙O相切；（2）证明见解析；（3）．

【解析】

试题分析：（1）结论：BC与⊙O相切，连接OD只要证明OD∥AC即可．

（2）欲证明△ABD∽△DBE，只要证明∠BDE=∠DAB即可．

（3）在Rt△ODB中，由cosB==，设BD=k，OB=3k，利用勾股定理列出方程求出k，再利用DO∥AC，得列出方程即可解决问题．

试题解析：（1）结论：BC与⊙O相切．

证明：如图连接OD．

∵OA=OD，∴∠OAD=∠ODA，∵AD平分∠CAB，∴∠CAD=∠DAB，∴∠CAD=∠ADO，∴AC∥OD，∵AC⊥BC，∴OD⊥BC，∴BC是⊙O的切线．

（2）∵BC是⊙O切线，∴∠ODB=90°，∴∠BDE+∠ODE=90°，∵AE是直径，∴∠ADE=90°，∴∠DAE+∠AED=90°，∵OD=OE，∴∠ODE=∠OED，∴∠BDE=∠DAB，∵∠B=∠B，∴△ABD∽△DBE．

（3）在Rt△ODB中，∵cosB==，设BD=k，OB=3k，∵OD2+BD2=OB2，∴4+8k2=9k2，∴k=2，∴BO=6，BD=，∵DO∥AC，∴，∴，∴CD=．