题目内容
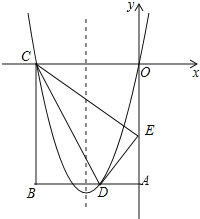
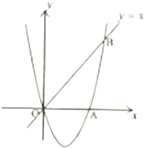
【题目】如图,经过原点![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于另一点
轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
(1)求这条抛物线的解析式;
(2)在第四象限内的抛物线上有一点![]() ,满足以
,满足以![]() ,
,![]() ,
,![]() 为顶点的三角形的面积为1,求点
为顶点的三角形的面积为1,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)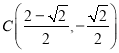 .
.
【解析】
(1)将B(2,m)代入y=x,求出B,再将A与B代入抛物线即可求函数解析式;
(2)过C作CD∥y轴,交x轴于点E,交OB于点D,过B作BF⊥CD于点,设C(t,2t2-3t),则E(t,0),D(t,t),可求OE=t,BF=2-t,CD=t-(2t2-3t)=-2t2+4t,再由S△OBC=S△CDO+S△CDB=![]() CDOE+
CDOE+![]() CDBF=
CDBF=![]() (-2t2+4t)(t+2-t)=-2t2+4t,并且△OBC的面积为1,即可求出t的值,进而确定点C坐标;
(-2t2+4t)(t+2-t)=-2t2+4t,并且△OBC的面积为1,即可求出t的值,进而确定点C坐标;
解:(1)∵![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
把![]() 、
、![]() 两点坐标代入抛物线解析式可得
两点坐标代入抛物线解析式可得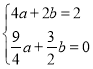 ,
,
解得![]() ,
,
∴抛物线解析式为![]() ;
;
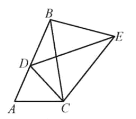
(2)如图1,过![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,

∵点![]() 是抛物线上第四象限的点,
是抛物线上第四象限的点,
∴可设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 的面积为1,
的面积为1,
∴![]() ,
,
解得![]() ,
,![]()
当![]() 时,
时,![]() (舍去);
(舍去);
当![]() 时,
时,![]() ,
,
∴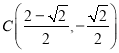 ;
;

练习册系列答案
相关题目