题目内容
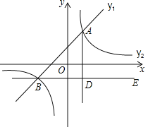
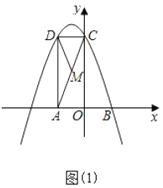
【题目】如图1,抛物线y![]() 2
2![]() 与x轴相交于A、B两点(点A在点B的右侧),与y轴相交于点C,对称轴与x轴相交于点H,与AC相交于点T.
与x轴相交于A、B两点(点A在点B的右侧),与y轴相交于点C,对称轴与x轴相交于点H,与AC相交于点T.
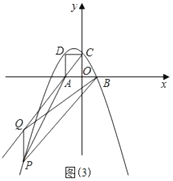
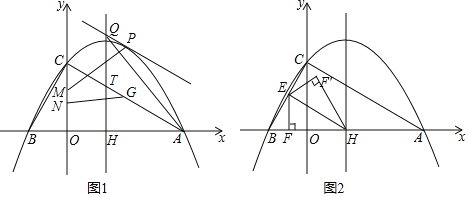
(1)点P是线段AC上方抛物线上一点,过点P作PQ∥AC交抛物线的对称轴于点Q,当△AQH面积最大时,点M、N在y轴上(点M在点N的上方),MN![]() ,点G在直线AC上,求PM+NG
,点G在直线AC上,求PM+NG![]() GA的最小值.
GA的最小值.
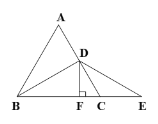
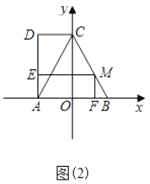
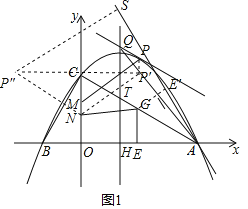
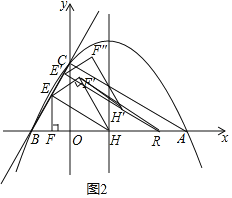
(2)点E为BC中点,EF⊥x轴于F,连接EH,将△EFH沿EH翻折得△EF'H,如图所示2,再将△EF'H沿直线BC平移,记平移中的△EF'H为△E'F″H',在平移过程中,直线E'H'与x轴交于点R,则是否存在这样的点R,使得△RF'H'为等腰三角形?若存在,求出R点坐标.
【答案】(1)![]() ;(2)点R的坐标为R(﹣4,0)或R(5,0)
;(2)点R的坐标为R(﹣4,0)或R(5,0)
【解析】
(1)由抛物线解析式可求![]() ,对称轴x=2,过P点作PT′∥QT,由PQ∥AC可知,四边形QTT′P是平行四边形,QT=PT’,因为HT为定值,所以PT′最大时,△AQH面积最大,由此构建二次函数,求出点P坐标,过点G作GE⊥x轴于E,作x轴关于直线AC的对称直线l,E的对称点为E′,将PM沿y轴向下平移
,对称轴x=2,过P点作PT′∥QT,由PQ∥AC可知,四边形QTT′P是平行四边形,QT=PT’,因为HT为定值,所以PT′最大时,△AQH面积最大,由此构建二次函数,求出点P坐标,过点G作GE⊥x轴于E,作x轴关于直线AC的对称直线l,E的对称点为E′,将PM沿y轴向下平移![]() 个单位至P′N,作点P′关于y轴的对称点P″,过P″作P″S⊥l于S,则有PM+NG
个单位至P′N,作点P′关于y轴的对称点P″,过P″作P″S⊥l于S,则有PM+NG![]() GA=P″N+NG+GE′≥P″S,求出P″S即可;
GA=P″N+NG+GE′≥P″S,求出P″S即可;
(2)先求得点E,F,F′,H′,R的坐标,根据△RF'H'为等腰三角形,分三种情况分别求解即可.
(1)如图1,抛物线y![]() 2
2![]() 与x轴相交于A、B两点(点A在点B的右侧),
与x轴相交于A、B两点(点A在点B的右侧),
∴A(6,0);B(﹣2,0);C(0,2![]() ),
),
∴直线AC的解析式为:![]() ,
,
∵tan∠CAO![]() ,
,
∴∠CAO=30°
过P点作PT′∥QT,交AC于T′,
设P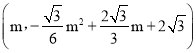 ,T′
,T′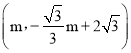 ,
,
则PT′![]() m+2
m+2![]() (
(![]() m+2
m+2![]() )
)![]() (m﹣3)2
(m﹣3)2![]()
∵PQ∥AC,
∴四边形QTT′P是平行四边形,
∴QT=PT′,
当△AQH面积最大时,HQ最大,即PT′最大,
即m=3时,△AQH面积最大,
此时P点坐标为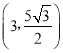 .
.
过点G作GE⊥x轴于E,作x轴关于直线AC的对称直线l,E的对称点为E′,将PM沿y轴向下平移![]() 个单位至P′N,作点P′关于y轴的对称点P″,过P″作P″S⊥l于S,则有
个单位至P′N,作点P′关于y轴的对称点P″,过P″作P″S⊥l于S,则有
PM+NG![]() GA=P″N+NG+GE′≥P″S
GA=P″N+NG+GE′≥P″S
∵P′(3,![]() ),P″与P′关于y轴对称
),P″与P′关于y轴对称
∴P″(﹣3,![]() ),
),
∵∠CAO=30°,直线l与x轴关于直线AC对称
∴∠CAS=∠CAO=30°,
∴∠SAO=60°
设直线l的解析式为y=kx+b,则k=﹣tan∠SAO=﹣tan60°![]()
∴y![]() x+b,将A(6,0)代入得:0
x+b,将A(6,0)代入得:0![]() 6+b,解得:b=6
6+b,解得:b=6![]() ,
,
∴直线l的解析式为y![]() x+6
x+6![]() ,
,
∵P″S⊥l
∴∠P″SA=90°
过点P″作P″K∥x轴交AS于K,则K(![]() ,
,![]() ),
),
∴P″K![]() (﹣3)
(﹣3)![]() ,
,
∵P″K∥x轴
∴∠P″KS=∠SAO=60°
∵![]() sin∠SAO
sin∠SAO
∴P″S=P″Ksin∠SAO![]() sin60°
sin60°![]() ,′
,′
∴PM+NG![]() GA的最小值
GA的最小值![]() ;
;
(2)∵y![]() 2
2![]() (x﹣2)2
(x﹣2)2![]()
∴抛物线对称轴为直线x=2,
∴H(2,0),
由(1)知:A(6,0);B(﹣2,0);C(0,2![]() ),
),
∵点E为BC中点,EF⊥x轴于F,
∴E(﹣1,![]() ),F(﹣1,0)
),F(﹣1,0)
∴F′(![]() ,
,![]() )
)
∵![]()
∴△EF′H沿直线BC平移,各个点横纵坐标变化为![]() ,设△EF′H沿直线BC平移后的△E′F″H′各顶点坐标分别为E′(﹣1+t,
,设△EF′H沿直线BC平移后的△E′F″H′各顶点坐标分别为E′(﹣1+t,![]() t),H′(2+t,
t),H′(2+t,![]() t)
t)
则直线E′H′解析式为y![]() x
x![]() t,令y=0,则x=2+4t
t,令y=0,则x=2+4t
∴R(2+4t,0),
∴H′R2=[(2+t)﹣(2+4t)]2+(![]() t﹣0)2=12t2,
t﹣0)2=12t2,
H′F′2=[2+t![]() )]2+(
)]2+(![]() t
t![]() )2=4t2﹣6t+9,
)2=4t2﹣6t+9,
F′R2![]() 16t2+12t+9,
16t2+12t+9,
∵△RF'H'为等腰三角形,
∴H′R2=H′F′2或H′F′2=F′R2或F′R2=H′R2,
①当H′R2=H′F′2时,则12t2=4t2﹣6t+9,解得:t1![]() ,t2
,t2![]()
此时,R(﹣4,0)或R(5,0)
②当H′F′2=F′R2时,则4t2﹣6t+9=16t2+12t+9,解得:t=0或![]() ,
,
t=0不符合题意,t![]() 与①重复
与①重复
③当F′R2=H′R2时,16t2+12t+9=12t2,解得:t1=t2![]() ,与①重复
,与①重复
综上所述,点R的坐标为R(﹣4,0)或R(5,0).

【题目】欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 | 三棱锥 | 三棱柱 | 正方体 | 正八面体 |
图形 |
|
|
|
|
顶点数V | 4 | 6 | 8 | |
棱数E | 6 | 12 | ||
面数F | 4 | 5 | 8 |
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.