题目内容
【题目】如图,在四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() .
.
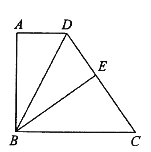
(1)求证: ![]() .
.
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;( 2) AB=8.
【解析】试题分析:(1)利用已知条件证明△ABD≌△EBD,根据确定三角形的对应边相等得到DA=DE;
(2)由△ABD≌△EBD,得到AD=DE=4,从而求得CE=6,在Rt△BCE中,利用勾股定理求得BE2=BC2-CE2=8,即可解答.
试题解析:(1)∵AB⊥AD,BE⊥DC
∴∠A=∠BED=90°,
∵BC=CD
∴∠DBC=∠BDC,
∵AD∥BC
∴∠DBC=∠ADB,
∴∠BDC=∠ADB,
在△ABD和△EBD中,
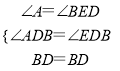 ,
,
∴△ABD≌△EBD,
∴DA=DE.
(2)∵△ABD≌△EBD,
∴AD=DE=4,
∵BC=CD=10,
∴CE=6,
在Rt△BCE中,
BE2=BC2-CE2=8,
∴AB=BE=8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


