äãá¢áÖàï
Àƒäãá¢À¢àÓë¥È˜åÖ![]() øÅȘ
øÅȘ ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cmȘà¶Ñ₤çÐ
=3 cmȘà¶Ñ₤çÐ![]() ÇÆçÐ
ÇÆçÐ![]() ¢ˆò¥È˜¯Ç
¢ˆò¥È˜¯Ç![]() çáôñƒÑåùÑ₤ȘúØùìÑàöˆû¢ûŠ1 cmȘèÒ°—ñÂçáòÝ¥ðöˆ
çáôñƒÑåùÑ₤ȘúØùìÑàöˆû¢ûŠ1 cmȘèÒ°—ñÂçáòÝ¥ðöˆ![]() s.
s.
(1)úµ°—ñÂ2s¤µÈ˜ ![]() çáûÌ£».
çáûÌ£».
(2) ![]() öˆ¤öøçòÝȘ
öˆ¤öøçòÝȘ ![]() öˆçàî■໧úÅö?
öˆçàî■໧úÅö?
(3)êÚÆÅØ£çÐ![]() ȘÇÆçÐ
ȘÇÆçÐ![]() ¢ˆò¥È˜¯Ç
¢ˆò¥È˜¯Ç![]() çáôñƒÑåùÑ₤ȘúØùìÑàöˆû¢ûŠ2 cmȘà¶
çáôñƒÑåùÑ₤ȘúØùìÑàöˆû¢ûŠ2 cmȘà¶![]() ê§çÐë˜òÝ°—ñÂȘçÝ
ê§çÐë˜òÝ°—ñÂȘçÝ![]() øÅÆÅØ£çÐç§ÇÿøíçÐòÝȘêÚØ£çÐØýëÈø¿åùÑ₤.çÝ
øÅÆÅØ£çÐç§ÇÿøíçÐòÝȘêÚØ£çÐØýëÈø¿åùÑ₤.çÝ![]() öˆ¤öøçòÝȘøÝüÔ
öˆ¤öøçòÝȘøÝüÔ![]() ¯î
¯î![]() çáøÉ°Êñø°èüÁçàçáê§ý¢ñø?
çáøÉ°Êñø°èüÁçàçáê§ý¢ñø?
ÀƒÇÞ¯¡À¢(1) ![]() çáûÌ£»öˆ
çáûÌ£»öˆ![]() cm2;(2) t=3s£·6s£·5.4s£·6.5sȘ
cm2;(2) t=3s£·6s£·5.4s£·6.5sȘ ![]() öˆçàî■໧úÅö;(3)çÝ
öˆçàî■໧úÅö;(3)çÝ![]() öˆ
öˆ![]() s£·
s£·![]() sòÝȘøÝüÔ
sòÝȘøÝüÔ![]() ¯î
¯î![]() çáøÉ°Êñø°èüÁçàçáê§ý¢ñø.
çáøÉ°Êñø°èüÁçàçáê§ý¢ñø.
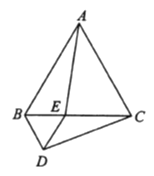
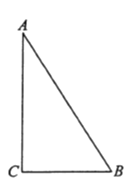
Àƒ§ãö—À¢òåäãñøö—Ȥȴ1Èˋâ«Æû¿Ç¿èÑ´âÚçû°—AC=4cmȘ§½Ñ½ÝÚòƒ°—APçá°ÊȘ§½Ñ½çû°—ÇÞ¯¡È£
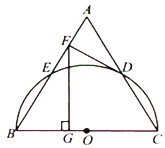
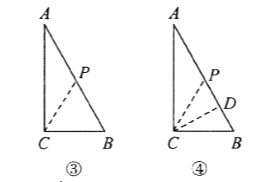
È´2Èˋñøê§øøúÕ¢—ȤÂìà¶PåÖÝÔACèüòÝȘBC=CP=6cmȘÇùòÝÆûçáòÝ¥ðöˆ6sÈ£ÂÖà¶PåÖABÝÔèüòÝȘÆÅà»øø¢èáÉȤià¶ò¿BP=CB=6cmȘÇùòÝAP=4cmȘPåùÑ₤çáôñ°äöˆ4+8=12cmȘÆûçáòÝ¥ðöˆ12òÝÈ£iiÈˋà¶CP=BC=6cmȘ¿»Cæ¼CDÀëABÆÖçÐDȘ¡ªƒïûÌ£»ñ´úµçû¡ÔCD=4.8cmȘúµ°—BP=2PD=7.2cmȘçû°—PåùÑ₤çáôñ°äöˆ18-7.2=10.8cmȘ¥Ç¢èçû°—§Ã¿«È£ÂÈÈˋà¶BP=CPȘå·ÀüPCB=ÀüBȘøÊ°—PA=PCçû°—PA=PB=5cmȘçû°—Pçáôñ°äöˆ13cmȘ¥Ç¢èçû°—§Ã¿«È£
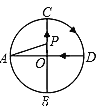
È´3Èˋñøê§øøúÕ¢—ȤÂìçÝPÀÂQû£üÁÆ—ú¯È¤PçÐæÔ¿»çáôñ°äöˆtȘQæÔ¿»çáôñ°äöˆ2tȘ¡ªƒïäãØãçû°—ñ§°äȘ§ãñ§°ä¥Ç¢èÈ£ÂÖçÝPÀÂQû£üÁÆ—¤µÈ¤çÝPçÐåÖABèüȘQåÖACèüȘå·AP=t-8ȘAQ=2t-16Ș¡ªƒïäãØãçû°—ñ§°äȘ§ãñ§°ä¥Ç¢èÈ£¥Ç¢èçû°—§Ã¿«ÈÛ
(1)àÓë¥ÂìȘطöˆ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cm
=3 cm
ùªØå![]() cm
cm
Ñ₤çÐ![]() ÇÆçÐ
ÇÆçÐ![]() ¢ˆò¥È˜¯Ç
¢ˆò¥È˜¯Ç![]() çáôñƒÑåùÑ₤ȘúØùìÑàöˆû¢ûŠ1 cmȘùªØå°—ñÂ2s¤µÈ˜
çáôñƒÑåùÑ₤ȘúØùìÑàöˆû¢ûŠ1 cmȘùªØå°—ñÂ2s¤µÈ˜ ![]() .
.
Ø·öˆ![]()
ùªØå![]() çáûÌ£»öˆ
çáûÌ£»öˆ![]() cm2.
cm2.
(2)ÂìàÓë¥ÂÖȘçÝçÐ![]() åÖÝÔ
åÖÝÔ![]() èüòÝȘ
èüòÝȘ ![]() cmȘÇùòÝ
cmȘÇùòÝ![]() Ș
Ș ![]() öˆçàî■໧úÅö;
öˆçàî■໧úÅö;
ÂÖçÝçÐ![]() åÖ
åÖ![]() ÝÔèüòÝȘÆÅà»øøúÕ¢—:
ÝÔèüòÝȘÆÅà»øøúÕ¢—:
Âþ)àÓë¥ÂÜȘà¶![]() cmȘÇùòÝ
cmȘÇùòÝ![]() cmȘçÐ
cmȘçÐ![]() åùÑ₤çáôñ°äöˆ
åùÑ₤çáôñ°äöˆ![]() (cm)ȘÇùòÝ
(cm)ȘÇùòÝ![]() Ș
Ș ![]() öˆçàî■໧úÅö;
öˆçàî■໧úÅö;
·)àÓë¥ÂÉȘà¶![]() cmȘ¿»çÐ
cmȘ¿»çÐ![]() æ¼ÅÝÝÔ
æ¼ÅÝÝÔ![]() çá¡Ô§£
çá¡Ô§£![]() ÆÖçÐ
ÆÖçÐ![]() Ș¡ªƒïûÌ£»ñ´úµçû¡Ôöˆ
Ș¡ªƒïûÌ£»ñ´úµçû¡Ôöˆ![]() cmȘùªØå
cmȘùªØå![]() cmȘùªØå
cmȘùªØå![]() cmȘùªØåçÐ
cmȘùªØåçÐ![]() åùÑ₤çáôñ°äöˆ
åùÑ₤çáôñ°äöˆ![]() (cm)ȘÇùòÝ
(cm)ȘÇùòÝ![]() Ș
Ș ![]() öˆçàî■໧úÅö
öˆçàî■໧úÅö
µ)àÓë¥ÂïȘà¶![]() ȘÇùòÝ
ȘÇùòÝ![]() ÆΡûöˆÅÝÝÔ
ÆΡûöˆÅÝÝÔ![]() çáøÅçÐȘçÐ
çáøÅçÐȘçÐ![]() åùÑ₤çáôñ°äöˆ
åùÑ₤çáôñ°äöˆ![]() (cm)ȘÇùòÝùªÆûçáòÝ¥ðöˆ
(cm)ȘÇùòÝùªÆûçáòÝ¥ðöˆ![]() sȘ
sȘ ![]() öˆçàî■໧úÅö.
öˆçàî■໧úÅö.
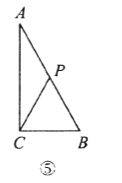
(3)àÓë¥ÂßȘçÝçÐ![]() åÖ
åÖ![]() èüȘçÐ
èüȘçÐ![]() åÖ
åÖ![]() èüòÝȘå·
èüòÝȘå·![]() Ș
Ș ![]() ȘùªØå
ȘùªØå![]() ȘùªØå
ȘùªØå![]() s;
s;
àÓë¥ÂÔȘçÝçÐ![]() åÖ
åÖ![]() èüȘçÐ
èüȘçÐ![]() åÖ
åÖ![]() èüòÝȘå·
èüòÝȘå·![]() Ș
Ș ![]() ȘùªØå
ȘùªØå![]() ȘùªØå
ȘùªØå![]() sȘùªØåçÝ
sȘùªØåçÝ![]() öˆ
öˆ![]() £·
£·![]() òÝȘøÝüÔ
òÝȘøÝüÔ![]() ¯î
¯î![]() çáøÉ°Êñø°èüÁçàçáê§ý¢ñø.
çáøÉ°Êñø°èüÁçàçáê§ý¢ñø.



 û«ÅÈ¢öäûüçêÅÇÞ¯¡
û«ÅÈ¢öäûüçêÅÇÞ¯¡