题目内容
【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.在数轴上若点A、B分别表示有理数a、b ,在数轴上A、B两点之间的距离AB=| a-b | .结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示﹣3和2的两点之间的距离是_____;数轴上表示 x 和 -3 两点之间的距离是_____;
(2)若a表示一个有理数,则|a+4|+|a﹣2|有最小值吗?若有,请求出最小值;若没有,请说明理由;
(3)当a =_____时,|a+4|+|a﹣1|+|a﹣2|的值最小,最小值是_____.
【答案】(1)5, ![]() ;(2) 有,最小值是6; (3) 1, 6
;(2) 有,最小值是6; (3) 1, 6
【解析】
(1)直接根据数轴上A、B两点之间的距离|AB|=|a-b|.代入数值运用绝对值即可求任意两点间的距离.
(2)代数式|a+4|+|a﹣2|表示数轴上一点到4、-2两点的距离的和,根据两点之间线段最短,进而得出答案.
(3)依据绝对值的几何意义回答即可.
解:(1)数轴上表示-3和2的两点之间的距离是|-3-2|=5,数轴上表示x和-3的两点之间的距离是|x-(-3)|=![]() .
.
(2)代数式|a+4|+|a﹣2|表示数轴上一点a到-4和2两点的距离和,根据两点之间线段最短可知,有最小值为:2-(-4)=6.
(3)①当a≤-4时,原式=-a-4-a+1-a+2 =-3a-1,a=-4时,最小值为11;
②当-4<a≤1时,原式=a+4-a+1-a+2=-a+7,a=1时,最小值为6;
③当1<a≤2时,原式=a+4+a-1-a+2=a+5,a=1时,最小值为6;
④当a>2时,原式=a+4+a-1+a-2=3a+1,a=2时,最小值为7;
综上,当a =1时,|a+4|+|a﹣1|+|a﹣2|的值最小,最小值是6.

 阅读快车系列答案
阅读快车系列答案【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: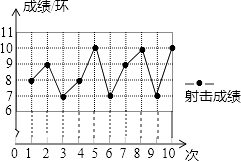
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.