��Ŀ����
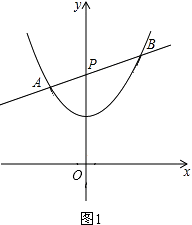
����Ŀ����֪���κ���ͼ��Ķ�������Ϊ��0��1�����ҹ��㣨��1�� ![]() ����ֱ��y=kx+2��y���ཻ�ڵ�P������κ���ͼ���ڲ�ͬ������A��x1 �� y1����B��x2 �� y2���� ��ע���ڽ�������У���Ҳ�����Ķ�����IJ��ϣ�
����ֱ��y=kx+2��y���ཻ�ڵ�P������κ���ͼ���ڲ�ͬ������A��x1 �� y1����B��x2 �� y2���� ��ע���ڽ�������У���Ҳ�����Ķ�����IJ��ϣ�
�����Ķ�����
�κ�һ��һԪ���η��̵ĸ���ϵ���Ĺ�ϵΪ�������ĺ͵���һ����ϵ���������ϵ���ıȵ��෴���������Ļ����ڳ������������ϵ���ıȣ�
������һԪ���η���ax2+bx+c=0������Ϊx1 �� x2 ��
��x1+x2=�� ![]() ��x1x2=
��x1x2= ![]()
������������ֹ�ϵ����ʱ����ʹ�����Ϊ��
�������ⷽ�̣���x2��3x=15�����ĺ������
�⣺ԭ���̱�Ϊ��x2��3x��15=0
��һԪ���η��̵ĸ���ϵ���й�ϵ��x1+x2=�� ![]() ��x1x2=
��x1x2= ![]()
��ԭ��������֮��=�� ![]() =3������֮��=
=3������֮��= ![]() =��15��
=��15��
��1����ö��κ����Ľ���ʽ��
��2���ԣ�1���еĶ��κ��������Ա���xȡֵ��Χ�ک�1��x��3ʱ����д���亯��ֵy��ȡֵ��Χ��������˵�����ɣ�
��3����֤���ڴ˶��κ���ͼ���·���y���ϣ��ش��ڶ���G��ʹ��ABG������Բ��Բ������y���ϣ������GAB�������Сֵ��
���𰸡�
��1���⣺���ڶ��κ���ͼ��Ķ�������Ϊ��0��1����
��˶��κ����Ľ���ʽ����Ϊy=ax2+1��
��������y=ax2+1���㣨��1�� ![]() ����
����
�� ![]() =a+1��
=a+1��
��ã�a= ![]() ��
��
����κ����Ľ���ʽΪ��y= ![]() x2+1
x2+1
��2���⣺��x=��1ʱ��y= ![]() ��
��
��x=0ʱ��y=1��
��x=3ʱ��y= ![]() ��32+1=
��32+1= ![]() ��
��
���ͼ1�ɵã�����1��x��3ʱ��y��ȡֵ��Χ��1��y�� ![]()
��3����֤��������A��y��ĶԳƵ�A�䣬����BA�䲢�ӳ�����y���ڵ�G������AG����ͼ2��
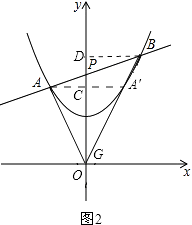
���A������������ϣ��ҡ�AGP=��BGP��
���ABG������Բ��Բ������y���ϣ�
�ߵ�A������Ϊ��x1��y1����
���A�����������x1��y1����
�ߵ�A��x1��y1����B��x2��y2����ֱ��y=kx+2�ϣ�
��y1=kx1+2��y2=kx2+2��
���A�����������x1��kx1+2������B��������x2��kx2+2����
��ֱ��BG�Ľ���ʽΪy=mx+n�����G������Ϊ��0��n����
�ߵ�A�䣨��x1��kx1+2����B��x2��kx2+2����ֱ��BG�ϣ�
�� ![]() ��
��
��ã� 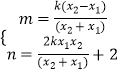 ��
��
��A��x1��y1����B��x2��y2����ֱ��y=kx+2��������y= ![]() x2+1�Ľ��㣬
x2+1�Ľ��㣬
��x1��x2�Ƿ���kx+2= ![]() x2+1��x2��4kx��4=0������ʵ������
x2+1��x2��4kx��4=0������ʵ������
���ɸ���ϵ���Ĺ�ϵ�ɵã�x1+x2=4k��x1x2=��4��
��n= ![]() =��2+2=0��
=��2+2=0��
���G��������0��0����
���ڴ˶��κ���ͼ���·���y���ϣ����ڶ���G��0��0����ʹ��ABG������Բ��Բ������y���ϣ�
�ڽ⣺����A��AC��OP������ΪC������B��BD��OP������ΪD����ͼ2��

��ֱ��y=kx+2��y���ཻ�ڵ�P��
���P��������0��2����
��PG=2��
��S��ABG=S��APG+S��BPG
= ![]() PGAC+
PGAC+ ![]() PGBD
PGBD
= ![]() PG��AC+BD��
PG��AC+BD��
= ![]() ��2������x1
��2������x1
=x2��x1
= ![]()
= ![]()
= ![]()
=4 ![]() ��
��
�൱k=0ʱ��S��ABG��С����СֵΪ4��
���GAB�������СֵΪ4��
����������1������κ�������ʽΪy=ax2+1�����ڵ㣨��1�� ![]() ���ڶ��κ���ͼ���ϣ��Ѹõ���������y=ax2+1���������a���Ӷ�������κ����Ľ���ʽ����2���ȷֱ����x=��1��x=0��x=3ʱy��ֵ��Ȼ����ͼ��Ϳɵõ�y��ȡֵ��Χ����3������A��y��ĶԳƵ�A�䣬����BA�䲢�ӳ�����y���ڵ�G������AG����ͼ2�����A������������ϣ��ҡ�AGP=��BGP���ɴ˿ɵá�ABG������Բ��Բ������y���ϣ����ڵ�A��x1 �� y1����B��x2 �� y2����ֱ��y=kx+2�ϣ��Ӷ����Եõ���A������Ϊ��x1 �� kx1+2����A�������Ϊ����x1 �� kx1+2����B������Ϊ��x2 �� kx2+2������ֱ��BG�Ľ���ʽΪy=mx+n�����G������Ϊ��0��n�������ڵ�A�䣨��x1 �� kx1+2����B��x2 �� kx2+2����ֱ��BG�ϣ����ú���k��x1��x2�Ĵ���ʽ��ʾn������A��B��ֱ��y=kx+2��������y=
���ڶ��κ���ͼ���ϣ��Ѹõ���������y=ax2+1���������a���Ӷ�������κ����Ľ���ʽ����2���ȷֱ����x=��1��x=0��x=3ʱy��ֵ��Ȼ����ͼ��Ϳɵõ�y��ȡֵ��Χ����3������A��y��ĶԳƵ�A�䣬����BA�䲢�ӳ�����y���ڵ�G������AG����ͼ2�����A������������ϣ��ҡ�AGP=��BGP���ɴ˿ɵá�ABG������Բ��Բ������y���ϣ����ڵ�A��x1 �� y1����B��x2 �� y2����ֱ��y=kx+2�ϣ��Ӷ����Եõ���A������Ϊ��x1 �� kx1+2����A�������Ϊ����x1 �� kx1+2����B������Ϊ��x2 �� kx2+2������ֱ��BG�Ľ���ʽΪy=mx+n�����G������Ϊ��0��n�������ڵ�A�䣨��x1 �� kx1+2����B��x2 �� kx2+2����ֱ��BG�ϣ����ú���k��x1��x2�Ĵ���ʽ��ʾn������A��B��ֱ��y=kx+2��������y= ![]() x2+1�Ľ��㣬�ɸ���ϵ���Ĺ�ϵ�ɵã�x1+x2=4k��x1x2=��4���Ӷ����n=0������֤�����ڴ˶��κ���ͼ���·���y���ϣ����ڶ���G��0��0����ʹ��ABG������Բ��Բ������y���ϣ���S��ABG=S��APG+S��BPG �� ���Եõ�S��ABG=x2��x1=
x2+1�Ľ��㣬�ɸ���ϵ���Ĺ�ϵ�ɵã�x1+x2=4k��x1x2=��4���Ӷ����n=0������֤�����ڴ˶��κ���ͼ���·���y���ϣ����ڶ���G��0��0����ʹ��ABG������Բ��Բ������y���ϣ���S��ABG=S��APG+S��BPG �� ���Եõ�S��ABG=x2��x1= ![]() =4
=4 ![]() �����Ե�k=0ʱ��S��ABG��С����СֵΪ4��
�����Ե�k=0ʱ��S��ABG��С����СֵΪ4��
�����㾫�����������⣬������Ҫ�˽����ϵ���Ĺ�ϵ(һԪ���η���ax2+bx+c=0��a��0���ĸ��ɷ��̵�ϵ��a��b��c����������֮�͵��ڷ��̵�һ����ϵ�����Զ�����ϵ�����õ��̵��෴��������֮�����ڳ�������Զ�����ϵ�����õ���)����Ҫ����ȷ��һ�κ����ı���ʽ(ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����)�����֪ʶ���Ǵ���Ĺؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�������Ǵ���������˶�ϲ����ʳƷ������20��������ÿ��450��Ϊ������������Ľ����ֱ���������������ʾ����������IJ�ֵ��¼�����
ÿ����������IJ�ֵ��� | ��5 | ��2 | 0 | 1 | 3 | 6 |
���� | 1 | 4 | 3 | 4 | 5 | 3 |
��1����20�������У����ص�һ���������һ���ؼ��
��2����20�������ƽ�������ȱ���������٣�����ټ��
��3������20���������������