Question

【题目】如图，点A、B分别在y轴和x轴上，BC⊥AB（点C和点O在直线AB的两侧），点C的坐标为(4，n)过点C的反比例函数y=（x＞0）的图象交边AC于点D(n+，3)．

（1）求反比例函数的表达式；

（2）求点B的坐标．

Answer 1

【答案】（1）y=；（2）(2，0)

【解析】

（1）依据反比例函数图象上点的坐标特征，即可得到n的值，进而得出反比例函数的表达式；

（2）利用待定系数法即可得到直线CD的解析式为y=-x+4，进而得到点A的坐标，再根据△ABO∽△BCE，即可得到点B的坐标．

解：（1）∵反比例函数y=（x＞0）的图象经过点C（4，n）和点D（n+，3）．

∴

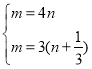
解得，

∴反比例函数的表达式为y=；

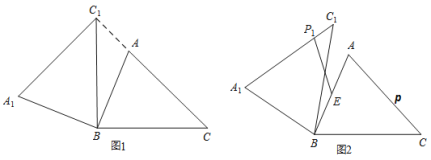
（2）如图，过C作CE⊥x轴于E，

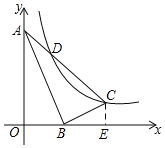
设直线CD的解析式为y=kx+b，

把点C（4，1），点D（，3）代入，可得

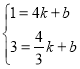，解得，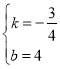

∴直线CD的解析式为y=-x+4，

令x=0，则y=4，

∴A（0，4），即AO=4，

设BO=x，则BE=4-x，

∵∠ABC=90°=∠AOB=∠BEC，

∴∠BAO+∠ABO=90°=∠CBE+∠ABO，

∴∠BAO=∠CBE，

∴△ABO∽△BCE，

∴，即，

解得x=2，

∴B（2，0）．