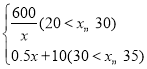��Ŀ����
����Ŀ���ڴ�����ȫ����������������ʡ�����������������У�������ˮ�����������ȹ���A��B������ˮ�����豸��20̨���Գ����ܱ���ˮ���д�������֪ÿ̨A���豸�۸�Ϊ12��Ԫ��ÿ̨B���豸�۸�Ϊ10��Ԫ��1̨A���豸��2̨B���豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A���豸��3̨B���豸ÿ�ܿ��Դ�����ˮ1080�֣�
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2��Ҫ��ʹ��ˮ�����������豸���ʽ���230��Ԫ����ÿ�ܴ�����ˮ�����ֲ�����4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
���𰸡���1��A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ240�֡�200�֣���2�����й���������������A����ˮ�����豸13̨��B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��
��������
��1��������������ȹ�ϵ��1̨A���豸ÿ�ܴ�������ˮ+2̨B���豸ÿ�ܴ�������ˮ=640�֣�2̨A���豸ÿ�ܴ�������ˮ+3̨B���豸ÿ�ܴ�������ˮ=1080�֣��ݴ���δ֪���з������ɣ�
��2���蹺��A����ˮ�����豸x̨�����ݹ����豸���ʽ���230��Ԫ����ÿ�ܴ�����ˮ�����ֲ�����4500�ּ����г�����x�IJ���ʽ�飬�ⲻ��ʽ�����x�ķ�Χ���ٽ��xΪ��������������й�������һ��������������
�⣺��1����A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮx�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮy�֣��������⣬
��![]() ����ã�
����ã�![]() ��
��
��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���蹺��A����ˮ�����豸x̨������B����ˮ�����豸��20��x��̨��
��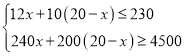 �� ��ã�12.5��x��15��
�� ��ã�12.5��x��15��
��xΪ��������x=13��14��15���ʹ������ֹ�����
��һ�ַ�������x=13ʱ��20��x=7�����ѵķ���Ϊ��13��12+7��10=226��Ԫ��
�ڶ��ַ�������x=14ʱ��20��x=6�����ѵķ���Ϊ��14��12+6��10=228��Ԫ��
�����ַ�������x=15ʱ��20��x=5�����ѵķ���Ϊ��15��12+5��10=230��Ԫ��
������A����ˮ�����豸13̨������B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��

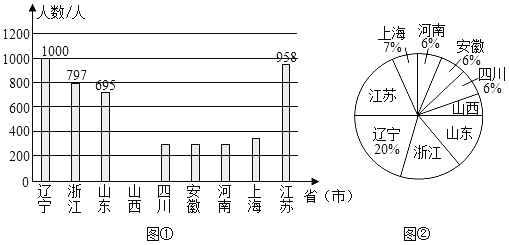
����Ŀ��������20�����ˣ�ij�������������������ͳ�����±���
����20������ijһ���������������ͳ�Ʊ�
��������ĸ��������� | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
�����������ˣ� | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ��������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������