题目内容
【题目】已知点A(1,a)在抛物线y=x2上.
(1)求A点的坐标;
(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)A(1,1);(2)存在,P1(![]() ,0),P2(-
,0),P2(-![]() ,0),P3(2,0),P4(1,0)
,0),P3(2,0),P4(1,0)
【解析】
试题(1)由点A(1,a)在抛物线y=x2上,代入即可求解;
(2)假设存在点P,根据△OAP是等腰三角形即可求解;
(1)∵点A(1,a)在抛物线y=x2上,
∴代入得:a=12=1;
∴A点的坐标为(1,1);
(2)假设存在点P,根据△OAP是等腰三角形,
①如图1,OA=AP时,此时OP=1+1=2,即P的坐标是(2,0);

②如图2,此时AP=0P=1,P的坐标是(1,0);
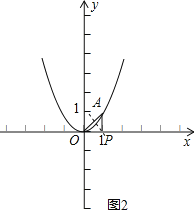
②如图3,OA=OP,此时符合条件的有两点P3,P4,OA=OP3=OP4=![]() ,
,
则P的坐标是(![]() ,0)或(-
,0)或(-![]() ,0);
,0);
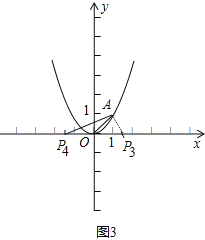
故P点坐标为:P1(![]() ,0),P2(-
,0),P2(-![]() ,0),P3(2,0),P4(1,0)
,0),P3(2,0),P4(1,0)

练习册系列答案
相关题目