题目内容
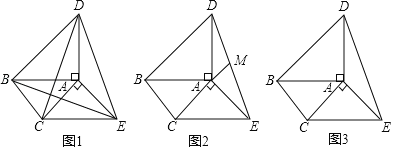
【题目】Rt△ABD和Rt△ACE如下3个图摆放,其中AB=AD,AC=AE.
(1)如图1,求证:BE=CD.
(2)如图2,M为DE中点,求证:BC=2AM.
(3)如图3,AB∥CE,AE∥BC,AC=![]() ,AB=2,直接写出四边形BCED的面积.
,AB=2,直接写出四边形BCED的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)5.
【解析】
(1)易证明△DAC≌△BAE,根据全等三角形对应线段相等即可得出结论;
(2)连接AM并延长至N,使MN=AM,连接DN、EN可证明四边形AEND是平行四边形,根据平行四边形的性质可证明△ABC≌△DAN,根据全等三角形的性质AN=BC,由此可得AM=![]() AN=
AN=![]() BC;
BC;
(3)由△ABC≌△DAN(SAS)可推出S△ABC=S△ADN=![]() S平行四边形AEND=S△ADE,由此可得出四边形BCED的面积=△BAD的面积+3△CAE的面积.
S平行四边形AEND=S△ADE,由此可得出四边形BCED的面积=△BAD的面积+3△CAE的面积.
解:(1)如图1中,
∵△ABD和△ACE是等腰直角三角形,
∴AB=AD,AE=AC,且∠DAB=∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠BAE=∠DAC,
在△DAC和△BAE中,
∵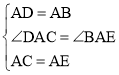 ,
,
∴△DAC≌△BAE(SAS),
∴CD=BE,
(2)如图2中,连接AM并延长至N,使MN=AM,连接DN、EN.
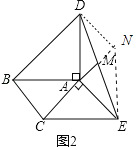
∵AM=MN,DM=ME,
∴四边形AEND是平行四边形,
∴DN=AE=AC,∠ADN+∠DAE=180°,
∵∠BAD=∠CAE=90°,
∴∠BAC+∠DAE=180°,
∴∠ADN=∠BAC,
在△ABC和△DAN中,
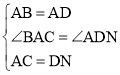 ,
,
∴△ABC≌△DAN(SAS),
∴AN=BC,
∴AM=![]() AN=
AN=![]() BC.
BC.
(3)如图3中,
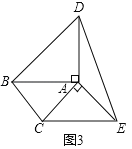
如图2中,由(2)可知:△ABC≌△DAN(SAS),
∴S△ABC=S△ADN=![]() S平行四边形AEND=S△ADE,
S平行四边形AEND=S△ADE,
∵AB∥CE,AE∥BC,
∴四边形ABCE是平行四边形,
∴BC=AE,AB=EC,∴S△ABC= S△ACE
∵AC=![]() ,AB=2,
,AB=2,
∴S四边形BCED=S△ABC+ S△ABD +S△AEC+ S△ADE=3 S△AEC + S△ABD =![]() .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案