Question

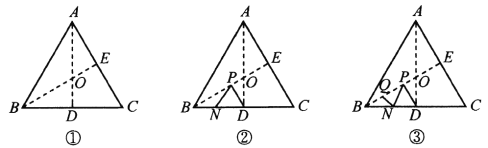
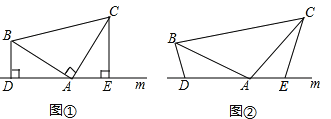
【题目】如图，将边长为6的正三角形纸片按如下顺序进行两次折叠，展开后，得折痕(如图①)，为其交点.

(1)探求与的数量关系，并说明理由;

(2)如图②，若分别为上的动点.

①当的长度取得最小值时，求的长度;

②如图③，若点在线段上，，则的最小值为 .

Answer 1

【答案】 (1) ； (2) ① ； ②.

【解析】

(1)根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°,得到AO=OB,根据直角三角形的性质即可得到结论;
(2)如图②,作点D关于BE的对称点D',过D'作D′N⊥BC于N交BE于P,则此时PN+PD的长度取得最小值,根据线段垂直平分线的想知道的BD=BD′,推出△BDD′是等边三角形,得到BN=BD=,于是得到结论;
(3)如图③,作Q关于BC的对称点Q',作D关于BE的对称点D',连接Q′D′,即为QN+NP+PD的最小值.根据轴对称的定义得到∠Q′BN=∠QBN=30°，∠QBQ′=60°,得到△BQQ′为等边三角形，△BDD′为等边三角形,解直角三角形即可得到结论.

（1）AO=2OD.

理由：∵△ABC是等边三角形，

∴∠BAO=∠ABO=∠OBD=30°

∴AO=OB，

∵BD=CD，

∴AD⊥BC，

∴∠BDO=90°，

∴OB=2OD，

∴AO=2OD.

（2）①如图，作点D关于BE的对称点D′，过D′作D′N⊥BC于N交BE于P，则此时PN+PD的长度取得最小值，

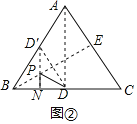
∵BE垂直平分DD′，

∴BD=BD′，

∵∠ABC=60°，

∴△BDD′是等边三角形，

∴BN=BD=，

∵∠PBN=30°，

∴，

∴PB=.

②如图，作Q关于BC的对称点Q′，作D关于BE的对称点D′，连接Q′D′，即为QN+NP+PD的值最小值，

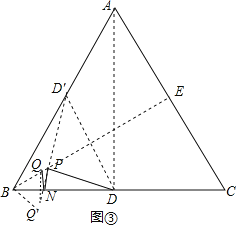
根据轴对称的定义可知：∠Q′BN=∠QBN=30°，∠QBQ′=60°，

∴△BQQ′为等边三角形，△BDD′为等边三角形，

∴∠D′BQ′=90°，

∴在Rt△D′BQ′中，

D′Q′= ，

∴QN+NP+PD的最小值= .