题目内容
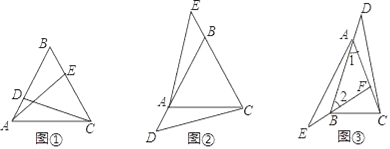
【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是_____,_____;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于_____度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3![]() 时,请直接写出线段CF的长的最大值是_____
时,请直接写出线段CF的长的最大值是_____
【答案】 CE=BD,CE⊥BD CE=BD,CE⊥BD 45°,. ![]()
【解析】解:(1)①∵AB=AC,∠BAC=90°,
∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠BAD=∠CAE,
∴△BAD≌△CAE,
∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
故答案为:CE=BD,CE⊥BD;
(2)(1)中的结论仍然成立.理由如下:如图2,
∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,
∵AB=AC,∠BAC=90°
∴∠CAE=∠BAD,
∴△ACE≌△ABD,
∴CE=BD,∠ACE=∠B,
∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
(3)
过A作AM⊥BC于M,过E点作EN垂直于MA延长线于N,如图3,
∵线段AD绕点A逆时针旋转90°得到AE,
∴∠DAE=90°,AD=AE,
∴∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA,
∴NE=AM,
∵CE⊥BD,即CE⊥MC,∴∠NEC=90°,
∴四边形MCEN为矩形,
∴NE=MC,∴AM=MC,
∴∠ACB=45°,
∵四边形MCEN为矩形,
∴Rt△AMD∽Rt△DCF,
∴![]() ,设DC=x,
,设DC=x,
∵在Rt△AMC中,∠ACB=45°,AC=3![]() ,
,
∴AM=CM=3,MD=3﹣x,∴![]() ,
,
∴CF=﹣![]() x2+x=﹣
x2+x=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时有最大值,最大值为
时有最大值,最大值为![]() .
.
故答案为:45°,![]() .
.