题目内容
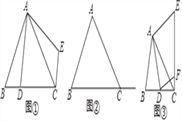
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=![]() ,tan∠DBC=
,tan∠DBC=![]() .
.
求:(1)边CD的长;
(2)△BCE的面积.

【答案】(1)CD=5;(2)![]()
【解析】试题分析:(1)先在Rt△ABC中,由余弦定理求得AC的值,进而理由勾股定理计算出BC,再在Rt△BCD中由正切定理解得CD的长;(2)通过做AB的平行线EH构造出相似三角形,由相似三角形对应边成比例可求得线段EH的长,最后理由三角形面积公式即可求解.
试题解析:(1)在Rt△ABC中, ![]() .
.
∴![]() ,
,
∴BC=![]() .
.
在Rt△BCD中, ![]() ,
,
∴CD=5.
(2)过点E作EH⊥BC,垂足为H,
∵∠ABC=∠BCD=90°,∴∠ABC+∠BCD=180°,∴CD//AB.
∴![]() .
.
∵∠EHC=∠ABC=90°,∴EH//AB,∴ ![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目