题目内容
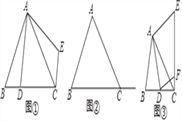
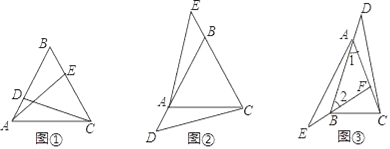
【题目】【感知】如图①,△ABC是等边三角形,点D、E分别在AB、BC边上,且AD=BE,易知:△ADC≌△BEA.
【探究】如图②,△ABC是等边三角形,点D、E分别在边BA、CB的延长线上,且AD=BE,△ADC与△BEA还全等吗?如果全等,请证明:如果不全等,请说明理由.
【拓展】如图③,在△ABC中,AB=AC,∠1=∠2,点D、E分别在BA、FB的延长线上,且AD=BE,若AF=![]() CF=2BE,S△ABF=6,则S△BCD的大小为 .
CF=2BE,S△ABF=6,则S△BCD的大小为 .
【答案】探究:△ADC与△BEA全等,理由见解析;拓展:S△BCD=13
【解析】试题分析:探究:利用平角的定义得出∠DAC=∠EBA即可得出结论;
拓展:先判断出△ADC≌△BEA,进而得出S△ADC=S△BEA,再利用同高的两三角形的面积的比等于底的比求出△ABE,△BCF的面积,即可得出结论.
试题解析:探究:△ADC与△BEA全等,
理由:在等边三角形ABC中,AB=AC,∠BAC=∠ABC=60°,
∴∠DAC=180°﹣∠BAC=120°,∠EBA=180°﹣∠ABC=120°,
∴∠DAC=∠EBA,
∵AD=BE,
∴△ADC≌△BEA;
拓展:∵∠1=∠2,
∴AF=BF,∠DAC=∠EBA,
∵AD=BE,AC=AB,
∴△ADC≌△BEA(SAS),
∴S△ADC=S△BEA,
∵AF=2BE,AF=BF,
∴BF=2BE,
∴S△ABE=![]() S△ABF=3(同高的两三角形的面积比是底的比),
S△ABF=3(同高的两三角形的面积比是底的比),
∴S△ADC=3,
∵AF=![]() CF,
CF,
∴S△BFC=![]() S△ABF=4(同高的两三角形的面积比是底的比),
S△ABF=4(同高的两三角形的面积比是底的比),
∴S△BCD=S△BCF+S△ABF+S△ADC=13,
故答案为13.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目