题目内容
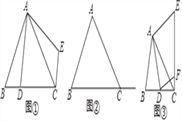
【题目】已知二次函数y=﹣![]() x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.

【答案】(1)M(![]() ,
, ![]() );(2)
);(2)![]() ,
, ![]()
【解析】试题分析:把点A(2,0)坐标代入二次函数![]() 解析式得出
解析式得出![]() ,再带回到
,再带回到![]() 中,配方化为顶点式即可得到顶点M的坐标;(2)先由tan∠MAN=2得出MN的长度,再分类讨论点B和N的位置关系,得出b的值,进而得出二次函数的解析式,A作AH⊥BC,根据正切函数定义即可得出∠ACB的正切值
中,配方化为顶点式即可得到顶点M的坐标;(2)先由tan∠MAN=2得出MN的长度,再分类讨论点B和N的位置关系,得出b的值,进而得出二次函数的解析式,A作AH⊥BC,根据正切函数定义即可得出∠ACB的正切值
解:(1)∵二次函数![]() 的图像经过点A(2,0),
的图像经过点A(2,0),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴顶点M的坐标为(![]() ,
, ![]() ).
).
(2)∵tan∠MAN=![]() 2,∴MN=2AN.
2,∴MN=2AN.
∵M(![]() ,
, ![]() ),∴ N(
),∴ N(![]() ,0),
,0),![]() .
.
①当点B在点N左侧时, AN= ![]() ,∴
,∴![]() ,
, ![]() .
.
不符合题意.
②当点B在点N右侧时, AN= ![]() , ∴
, ∴![]() ,
, ![]() .
.
∴二次函数的解析式为![]() .
.
∴点C(0,–10),∵点A、B关于直线MN对称,∴点B(10,0).
∵OB=OC=10,∴BC=10![]() ,∠OBC=45°.
,∠OBC=45°.
过点A作AH⊥BC,垂足为H,∵AB=8,∴AH=BH=4![]() ,∴CH=6
,∴CH=6![]() .
.
∴![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目