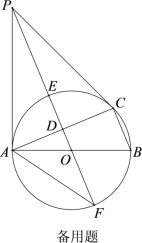
��Ŀ����
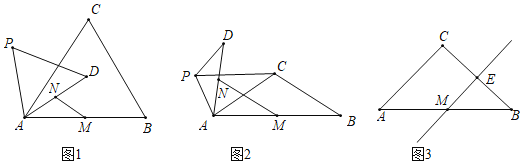
����Ŀ����ͼ������ABCD�У���ACB=30�㣬��һ��ֱ�����ǰ��ֱ�Ƕ���P�������Խ���AC��BD�Ľ��㴦���Ե�PΪ��ת����ת�����ǰ壬����֤���ǰ����ֱ�DZ߷ֱ����AB��BC���ڵ�ֱ���ཻ������ֱ�ΪE��F��
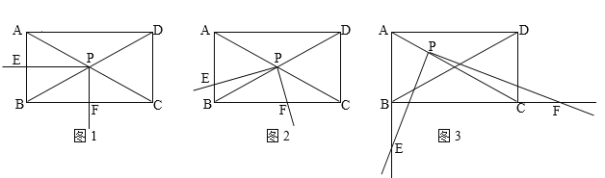
��1����PE��AB��PF��BCʱ����ͼ1����![]() ��ֵΪ������
��ֵΪ������
��2���ڣ�1���Ļ����ϣ��ֽ����ǰ��Ƶ�P��ʱ����ת![]() ��0�㣼
��0�㣼![]() ��60�㣩�ǣ���ͼ2����
��60�㣩�ǣ���ͼ2����![]() ��ֵ��
��ֵ��
��3�����루2�����ֻ�����±仯����P���߶�AC�ϣ���AP:PC=1:2,��ת�Ƕ�![]() ������60�㣼
������60�㣼![]() ��90��ʱ������ͼ3ʾ��
��90��ʱ������ͼ3ʾ��![]() ��ֵ�Ƿ�仯��֤����Ľ��ۣ�
��ֵ�Ƿ�仯��֤����Ľ��ۣ�
���𰸡���1��![]() ��2��
��2��![]() ��3��������
��3��������
��������
��1��֤����APE�ա�PCF����PE=CF����Rt��PCF�У���ֱ�����������![]() ��ֵ��
��ֵ��
��2�����ͼ1��ʾ���������ߣ�����ֱ�������Σ�֤����PME�ס�PNF�������ã�1���Ľ��ۣ����![]() ��ֵ��
��ֵ��
��3�����ͼ2��ʾ���������ߣ�����ֱ�������Σ�����֤����APM�ס�PCN�����![]() ��ֵ��Ȼ��֤����PME�ס�PNF���Ӷ���
��ֵ��Ȼ��֤����PME�ס�PNF���Ӷ���![]() =
=![]() ���
���![]() ��ֵ���루1����2������Ƚϣ�
��ֵ���루1����2������Ƚϣ�
![]() ��ֵ�����˱仯��
��ֵ�����˱仯��
�⣺(1)�߾���ABCD��
��AB��BC��PA=PC��
��PE��AB��BC��AB��
��PE��BC��
���APE=��PCF��
��PF��BC��AB��BC��
��PF��AB��
���PAE=��CPF��
���ڡ�APE���PCF�У�
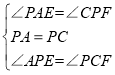
���APE�ա�PCF��ASA����
��PE=CF��
��Rt��PCF��![]() ��
��
��![]() .
.
�ʴ�Ϊ��![]()
(2) ���ͼ1������P��PM��AB�ڵ�M��PN��BC�ڵ�N����PM��PN��
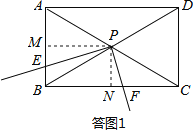
��PM��PN��PE��PF��
���EPM=��FPN��
�֡ߡ�PME=��PNF=90�㣬
���PME�ס�PNF
![]() =
=![]()
��(1)֪![]()
��![]()
![]() .
.
(3)�𣺱仯���������£�
֤�������ͼ2������P��PM��AB�ڵ�M��PN��BC�ڵ�N����PM��PN��PM��BC��PN��AB��
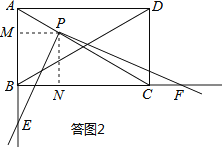
��PM��BC��PN��AB��
���APM=��PCN����PAM=��CPN��
���APM�ס�PCN��
![]() ���õ�CN=2PM
���õ�CN=2PM
��Rt��PCN��![]()
��![]()
��PM��PN��PE��PF��
���EPM=��FPN��
�֡ߡ�PME=��PNF=90����
���PME�ס�PNF��
��![]()
��![]() ��ֵ�����仯.
��ֵ�����仯.

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�