题目内容
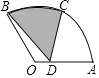
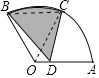
【题目】如图,在圆心角为120°的扇形OAB中,半径OA=2,C为![]() 的中点,D为OA上任意一点(不与点O、A重合),则图中阴影部分的面积为____.
的中点,D为OA上任意一点(不与点O、A重合),则图中阴影部分的面积为____.
【答案】![]() π.
π.
【解析】
连接OC,BC,由C为弧AB的中点,得到两条弧相等,进而得到所对的圆心角相等,再由OB=OC,得到三角形BOC为等边三角形,进而得到一对内错角相等,确定出BC与OA平行,利用同底等高三角形面积相等得到三角形BCD面积=三角形BOC面积,进而把阴影部分面积转化为扇形BOC面积,求出即可.
连接OC,BC,
∵圆心角为120°的扇形OAB中,C为![]() 的中点,
的中点,
∴∠BOC=∠AOC=60°,
∵OB=OC,
∴△BOC为等边三角形,
∴∠OCB=∠COA=60°,
∴BC∥OA,
∴由同底等高得到△BOC与△BCD面积相等,
∴S阴影=S弓形BC+S△BCD=S弓形BC+S△BOC=S扇形BOC=![]() ,
,
故答案为![]() π.
π.

【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息解答下列问题:
组别 | 阅读时间 | 频数(人数) |
|
| 8 |
|
| 20 |
|
| 24 |
|
|
|
|
|
|
|
| 4 |
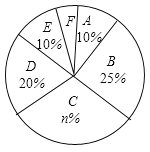
(1)图表中的![]() ______,
______,![]() ______;
______;
(2)扇形统计图中![]() 组所对应的圆心角为______度;
组所对应的圆心角为______度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?
【题目】如图,在![]() 中
中![]() ,
,![]() ,
,![]() 点P从点B出发,沿折线
点P从点B出发,沿折线![]() 运动,当它到达点A时停止,设点P运动的路程为
运动,当它到达点A时停止,设点P运动的路程为![]() 点Q是射线CA上一点,
点Q是射线CA上一点,![]() ,连接
,连接![]() 设
设![]() ,
,![]() .
.
![]() 求出
求出![]() ,
,![]() 与x的函数关系式,并注明x的取值范围;
与x的函数关系式,并注明x的取值范围;
![]() 补全表格中
补全表格中![]() 的值;
的值;
x | 1 | 2 | 3 | 4 | 6 |
| ______ | ______ | ______ | ______ | ______ |
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,并在x的取值范围内画出![]() 的函数图象:
的函数图象:
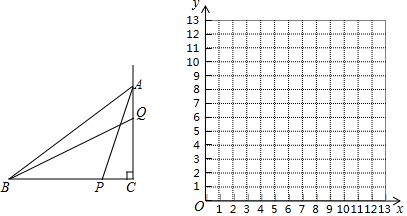
![]() 在直角坐标系内直接画出
在直角坐标系内直接画出![]() 函数图象,结合
函数图象,结合![]() 和
和![]() 的函数图象,求出当
的函数图象,求出当![]() 时,x的取值范围.
时,x的取值范围.