题目内容
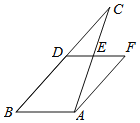
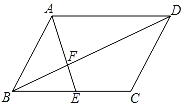
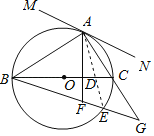
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,![]() =
=![]() ,BE分别交AD、AC延长线于点F、G.
,BE分别交AD、AC延长线于点F、G.
(1)过点A作直线MN,使得MN∥BG,判断直线MN与⊙O的位置关系,并说理.
(2)若AC=3,AB=4,求BG的长.
(3)连接CE,探索线段BD、CD与CE之间的数量关系,并说明理由.

【答案】(1)直线MN与⊙O相切,理由见解析;(2)BG=![]() ;(3)BD=CE+CD,理由见解析
;(3)BD=CE+CD,理由见解析
【解析】
(1)根据平行线的性质得到∠NAG=∠G,根据圆周角定理得出∠ABG=∠AEB,再由∠ABC+∠EBC=∠G+∠EAG得出∠ABC=∠G,进而得到∠NAG=∠ABC,由AB是直径得出∠BAC=90°,等量代换∠OAN=90°,求得OA⊥MN,即可得到结论;
(2)连接AE,根据圆周角定理得到∠AEB=∠ACB,根据等腰三角形的性质得到∠ABE=∠AEB,根据相似三角形的性质即可得到结论;
(3)连接CE,在BC上截取BH=CE,连接AH,根据全等三角形的判定方法得出△ABH≌△AEC(SAS),再根据全等三角形的性质即可得到结论.
解:(1)直线MN与⊙O相切,
理由:连接OA、AE

∵MN∥BG,
∴∠NAG=∠G,
∵![]() =
=![]() ,
,
∴AB=AE,∠ABG=∠AEB
∵∠EBC=∠EAC
∴∠ABC+∠EBC=∠G+∠EAG
∴∠ABC=∠G
∴∠NAG =∠ABC,
∵OA=OB
∴∠ABC=∠BAO=∠NAG
∵AB是直径
∴∠BAC=90°即∠BAO+∠OAC=90°
∴∠NAG+∠OAC=90°
即∠NAO=90°
∴OA⊥MN,
∴直线MN与⊙O相切;
(2)解:连接AE,
由(1)可知:∠ABC=∠G
∵∠BAC=∠GAB,
∴△ABC∽△AGB,
∴![]() ,
,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵AC=3,AB=4,
∴BC=5,
∴![]() ,
,
∴BG=![]() ;
;
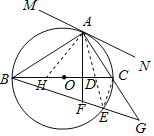
(3)解:BD=CE+CD,
理由:连接CE,
在BC上截取BH=CE,连接AH,
∵AB=AE,
又∵∠ABC=∠AEC,
∴△ABH≌△AEC(SAS),
∴AH=AC,
又∵AD⊥BC,
∴HD=CD,
∴BD=BH+HD=CE+CD.

【题目】为了调查某小区居民的用水情况,随机抽查了若干个家庭的![]() 月份用水量,结果如下表:
月份用水量,结果如下表:
月用水量(立方米) |
|
|
|
|
户数 |
|
|
|
|
根据上表解决下列问题:
(1)这组数据的众数是 ,中位数是 ;
(2)求这若干个家庭的![]() 月份平均用水量;
月份平均用水量;
(3)请根据(2)的结论估计该小区![]() 个家庭
个家庭![]() 月份总用水量.
月份总用水量.