题目内容
【题目】如图,直线y=kx+6与x轴、y轴分别交于点E,F.点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值,及一次函数解析式;
(2)若点P(x,y)是第二象限内的直线上的一个动点.当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,△OPA的面积为 ![]() ,并说明理由.
,并说明理由.
【答案】
(1)解:∵直线y=kx+6交于点E(﹣8,0),
∴0=﹣8k+6,
∴k= ![]() ,
,
∴这个一次函数解析式为y= ![]() x+6
x+6
(2)解:∵△OPA是以OA长度6为底边,P点的纵坐标为高的三角形,P(x, ![]() x+6)
x+6)
∴S△PAO= ![]() ×6×(
×6×( ![]() x+6)=
x+6)= ![]() x+18(﹣8<x<0);
x+18(﹣8<x<0);
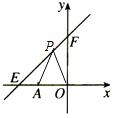
(3)解:∵△OPA的面积为 ![]() ,
,
∴ ![]() ,
,
∴x=﹣ ![]()
把 ![]() 代入一次函数
代入一次函数 ![]() ,得
,得 ![]()
∴当P点的坐标为( ![]() ,
, ![]() )时,△OPA的面积为
)时,△OPA的面积为 ![]() .
.
【解析】(1)把点E的坐标为(﹣8,0)代入y=kx+6求出k即可解决问题;(2)△OPA是以OA长度6为底边,P点的纵坐标为高的三角形,根据S△PAO= ![]() OAPy,列出函数关系式即可;、(3)利用(2)的结论,列出方程即可解决问题;
OAPy,列出函数关系式即可;、(3)利用(2)的结论,列出方程即可解决问题;
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握三角形的面积(三角形的面积=1/2×底×高)的相关知识才是答题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目